Math 20: Probability
About
probability distributions
python graph gallery
reproducible python code
main data analysis and math tools:
main ploting tools:
- Matplotlib
- Seaborn
- Plotly
Original code and data are in the Github Repository. Both the web page and the code will be updated irregularly.
Last updated: July 10
Slides 0629
-
How Much Does a Hershey Kiss Weight?
figure_hershey_dist(n, fsize, fs)
Slides 0701
-
US States
us_map_html(dict_state, target, title = None, country = 'US', cmap = tealrose)
us_map_png(dict_state, target, title = None, country = 'US', cmap = tealrose)
-
Histograms of Discrete Probability Distributions
-
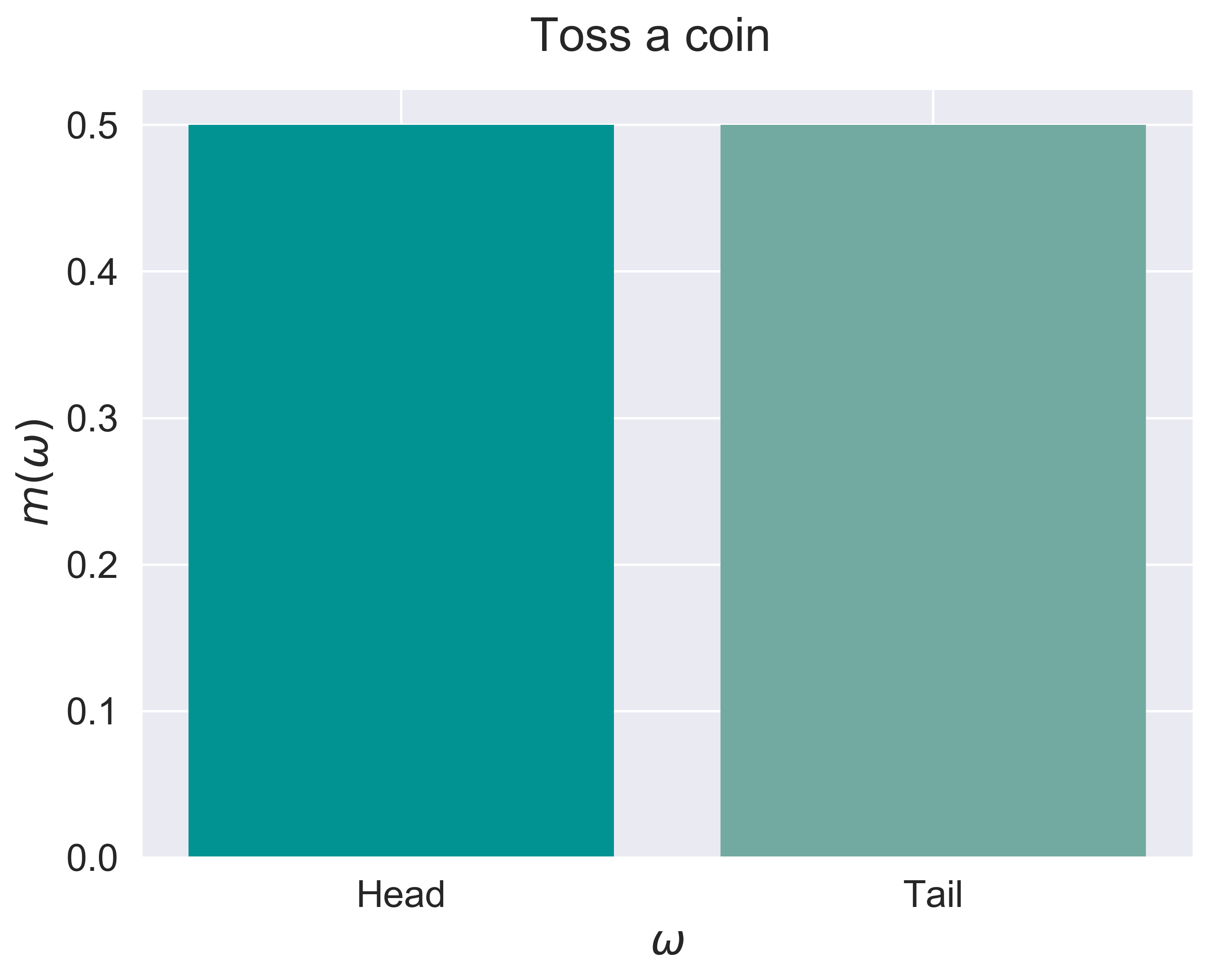
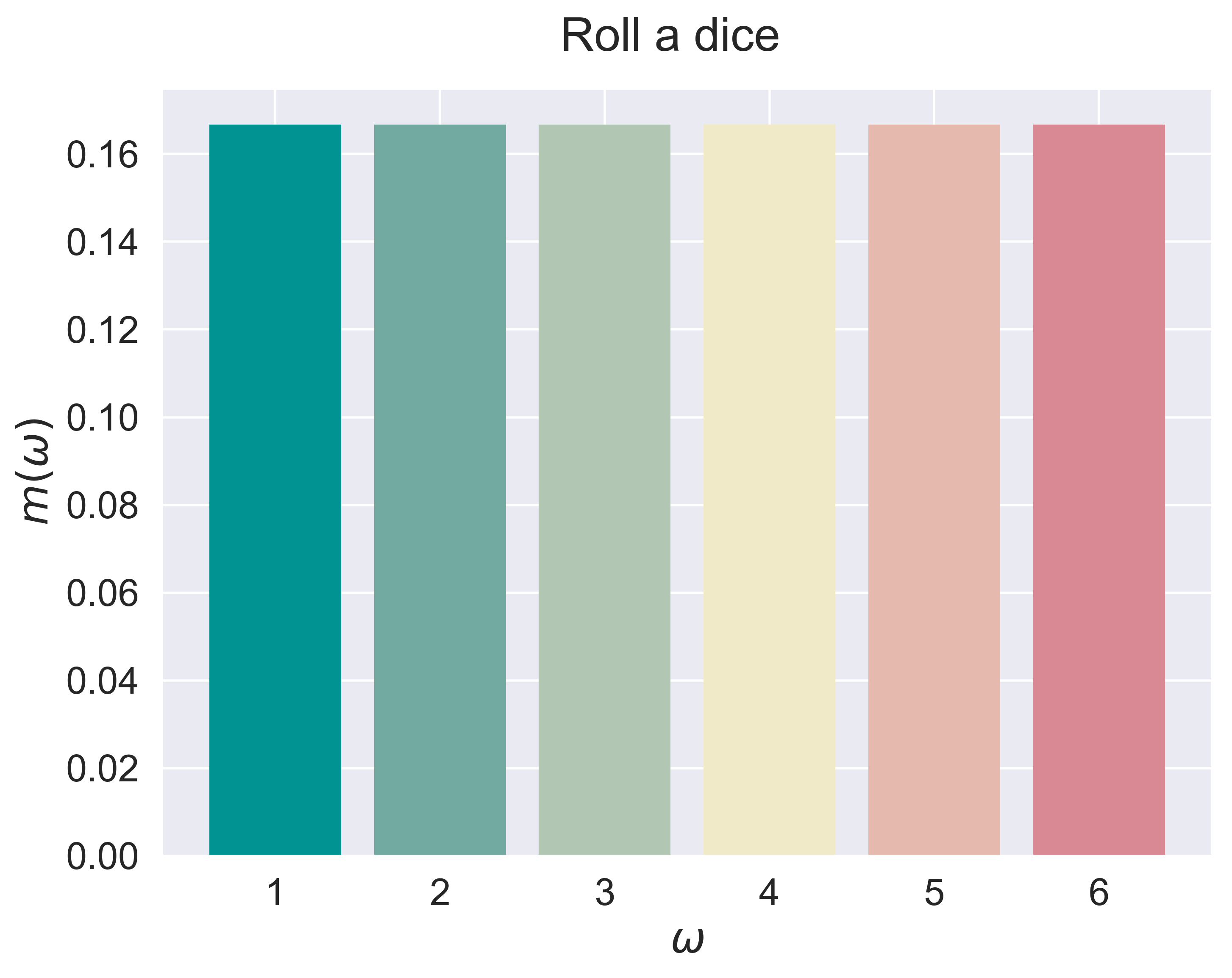
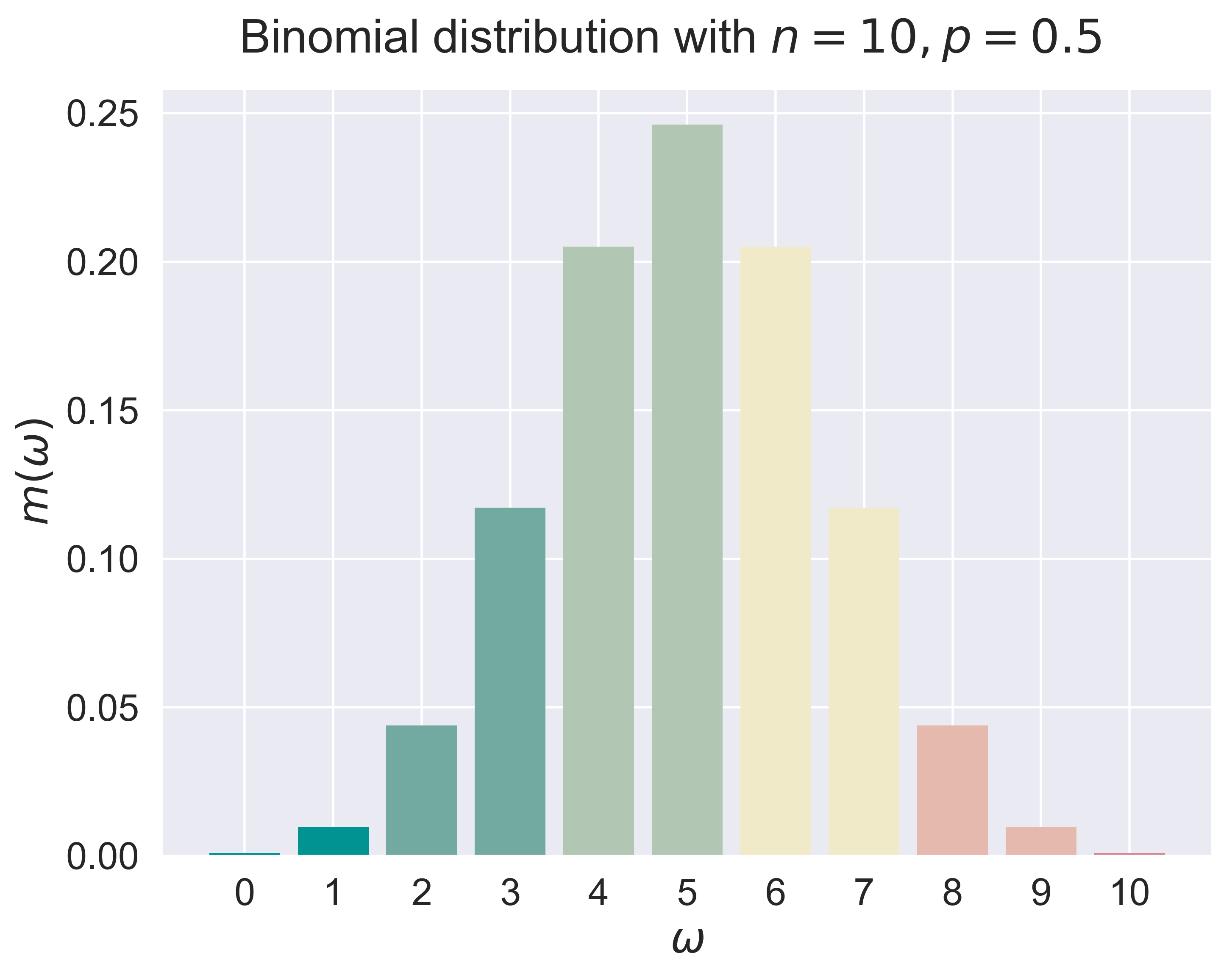
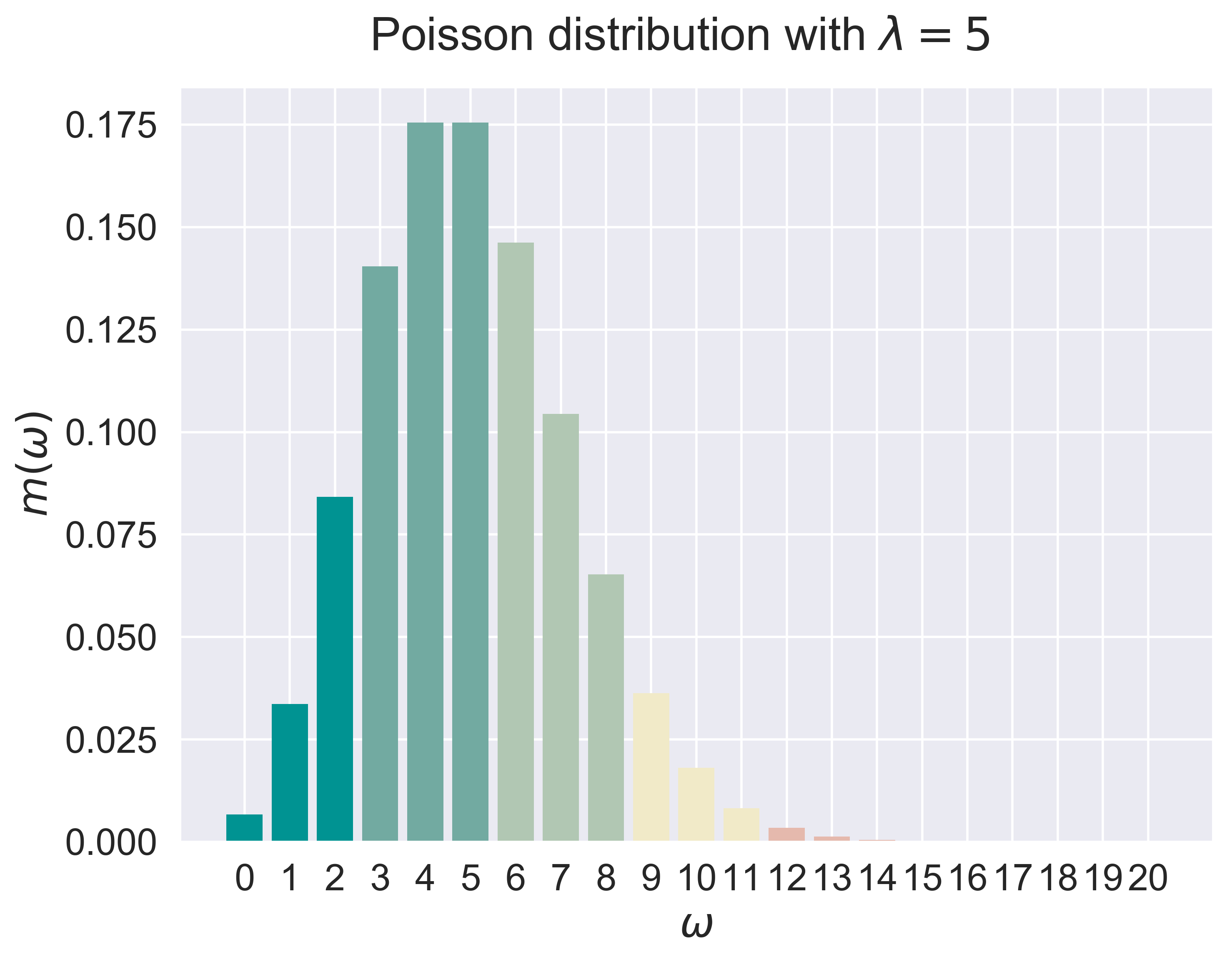
fundamental distributions
figure_discrete_hist(job = 'coin', fsize = (8, 6), fs = 20)
figure_discrete_hist(job = 'dice', fsize = (8, 6), fs = 20)
figure_discrete_hist(job = 'bino', fsize = (8, 6), fs = 20)
figure_discrete_hist(job = 'poisson', fsize = (8, 6), fs = 20)
-
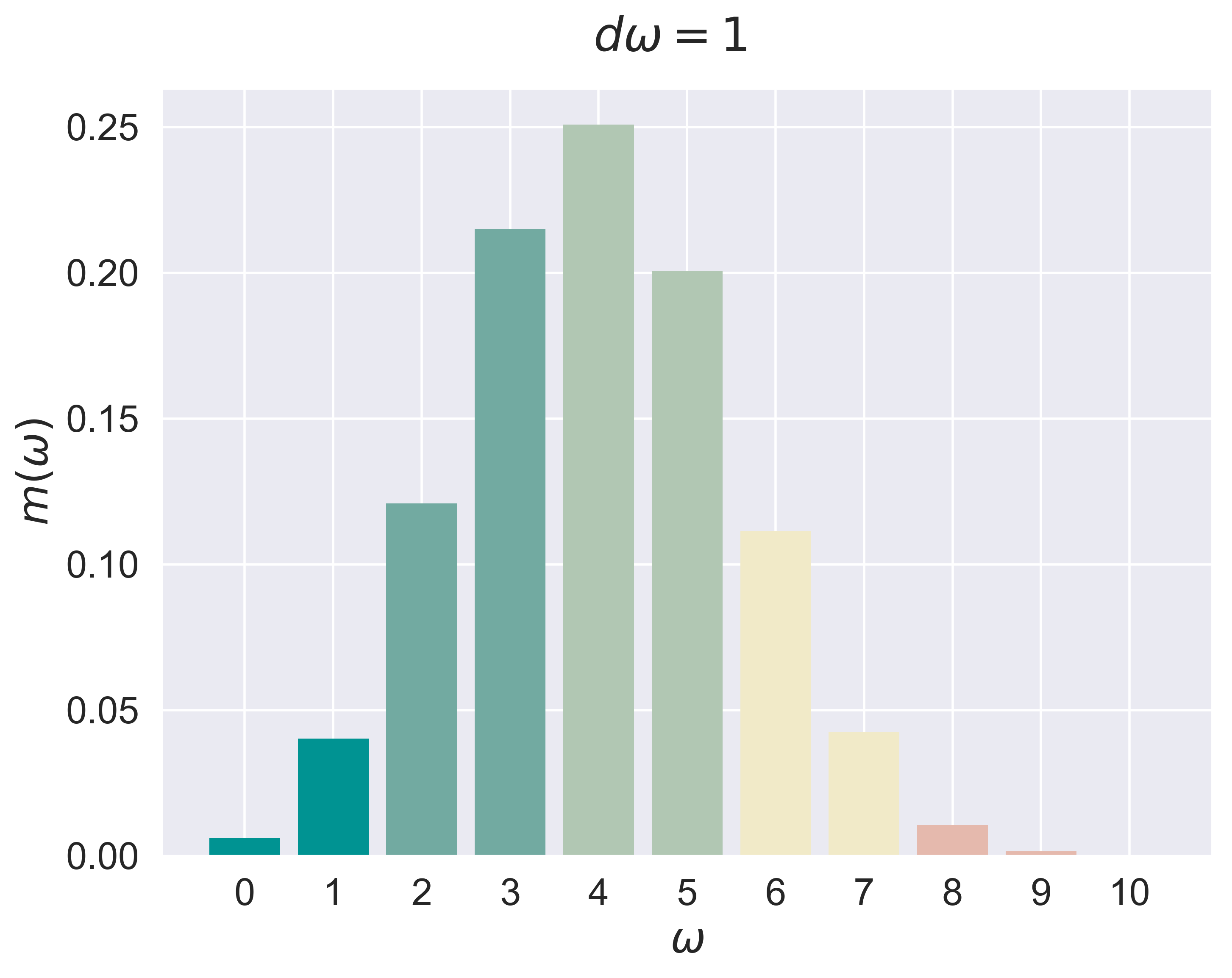
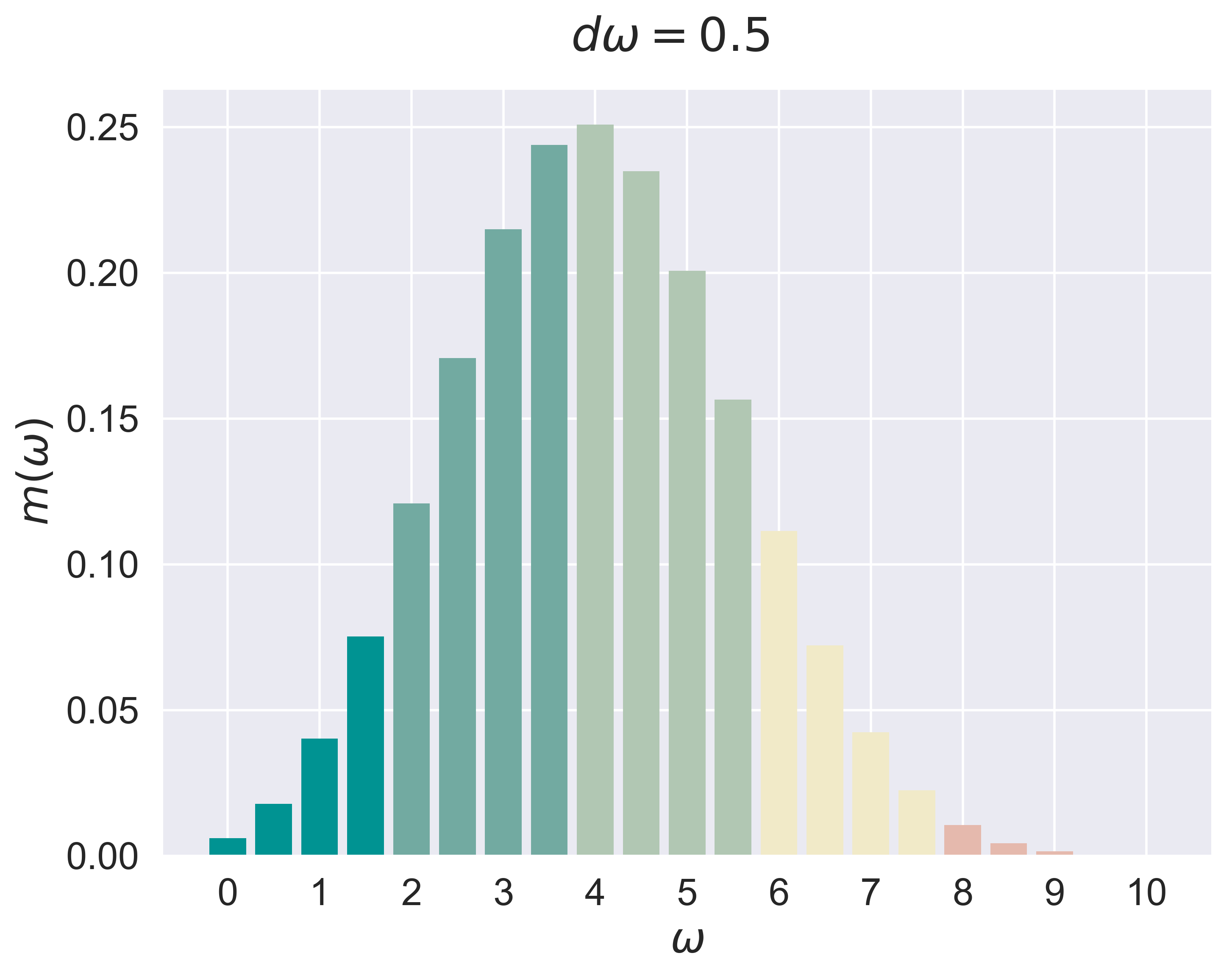
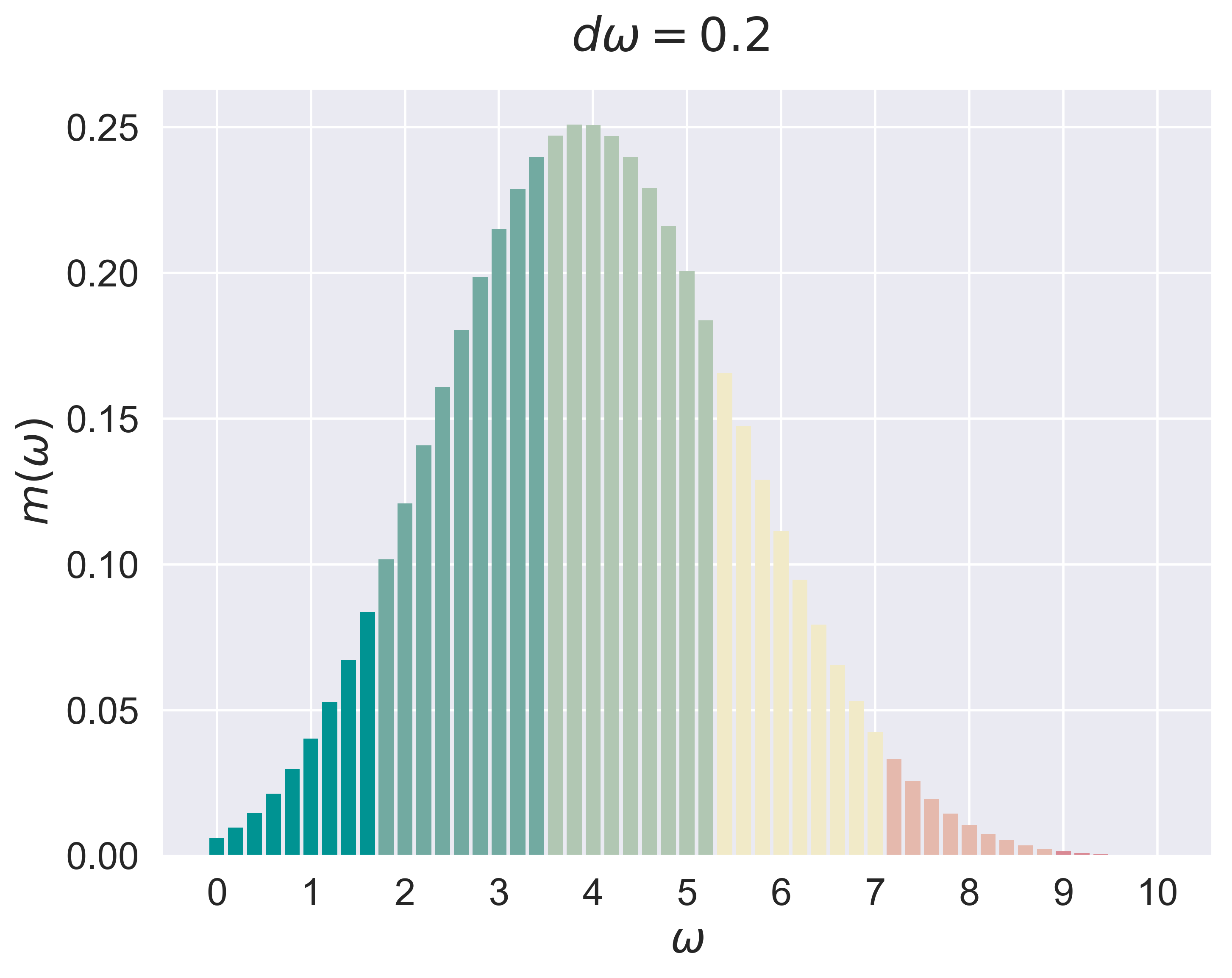
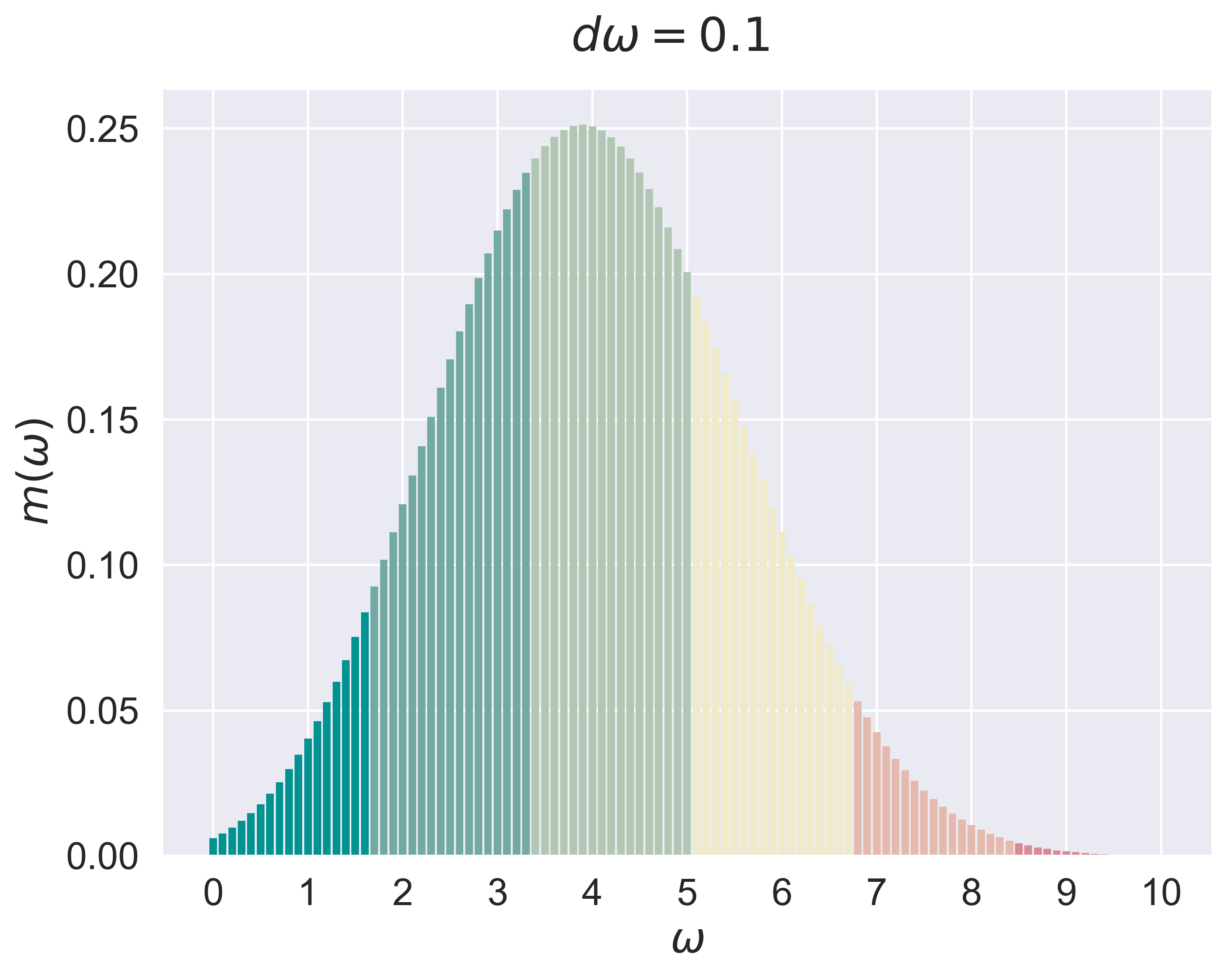
refinement of $d\omega$
figure_discrete_hist(job = 'bino_1', fsize = (8, 6), fs = 20)
figure_discrete_hist(job = 'bino_2', fsize = (8, 6), fs = 20)
figure_discrete_hist(job = 'bino_5', fsize = (8, 6), fs = 20)
figure_discrete_hist(job = 'bino_10', fsize = (8, 6), fs = 20)
-
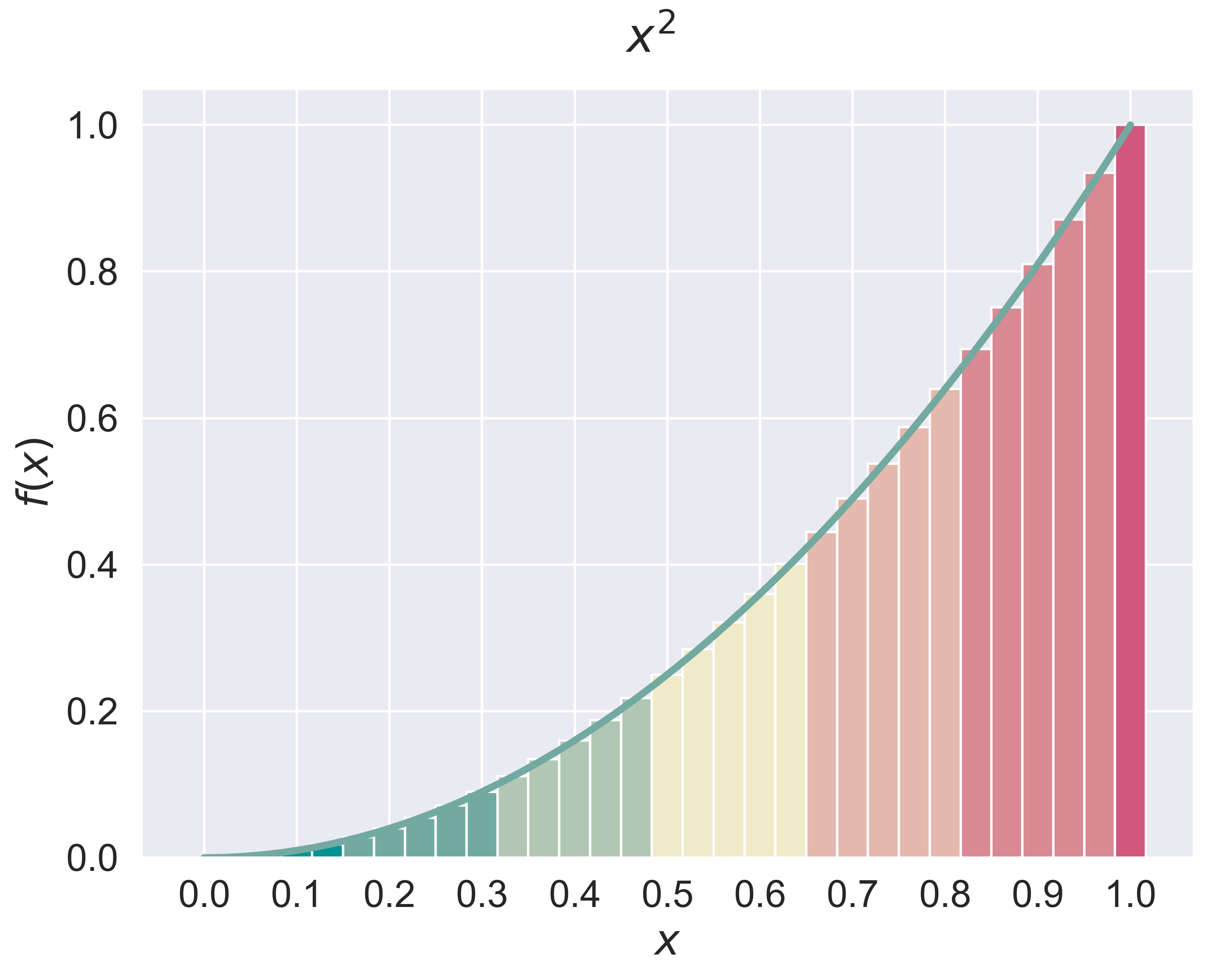
Riemann Sum of a Function
figure_riemann_sum(job = 'power', fsize = (8, 6), fs = 20)
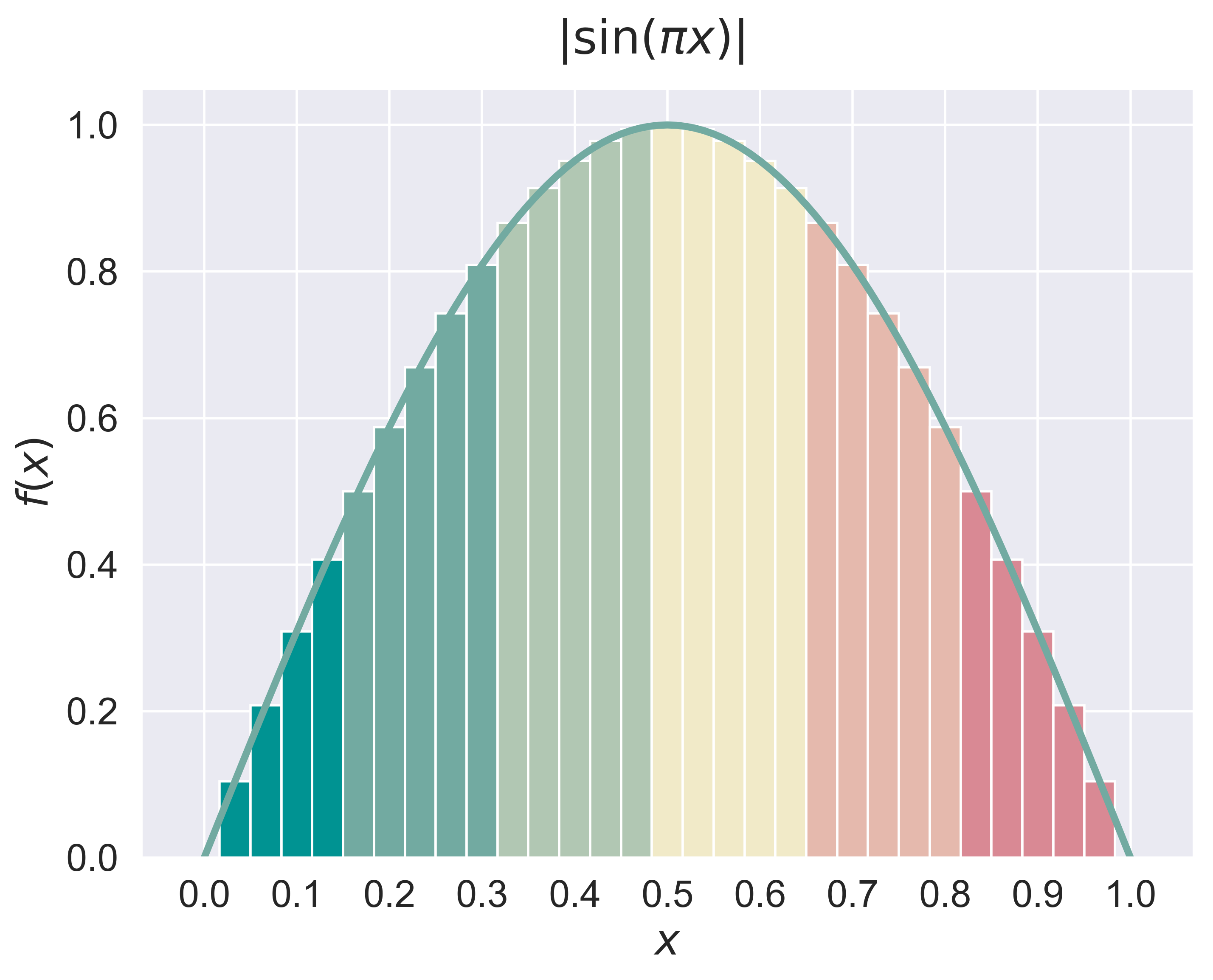
figure_riemann_sum(job = 'sin', fsize = (8, 6), fs = 20)
-
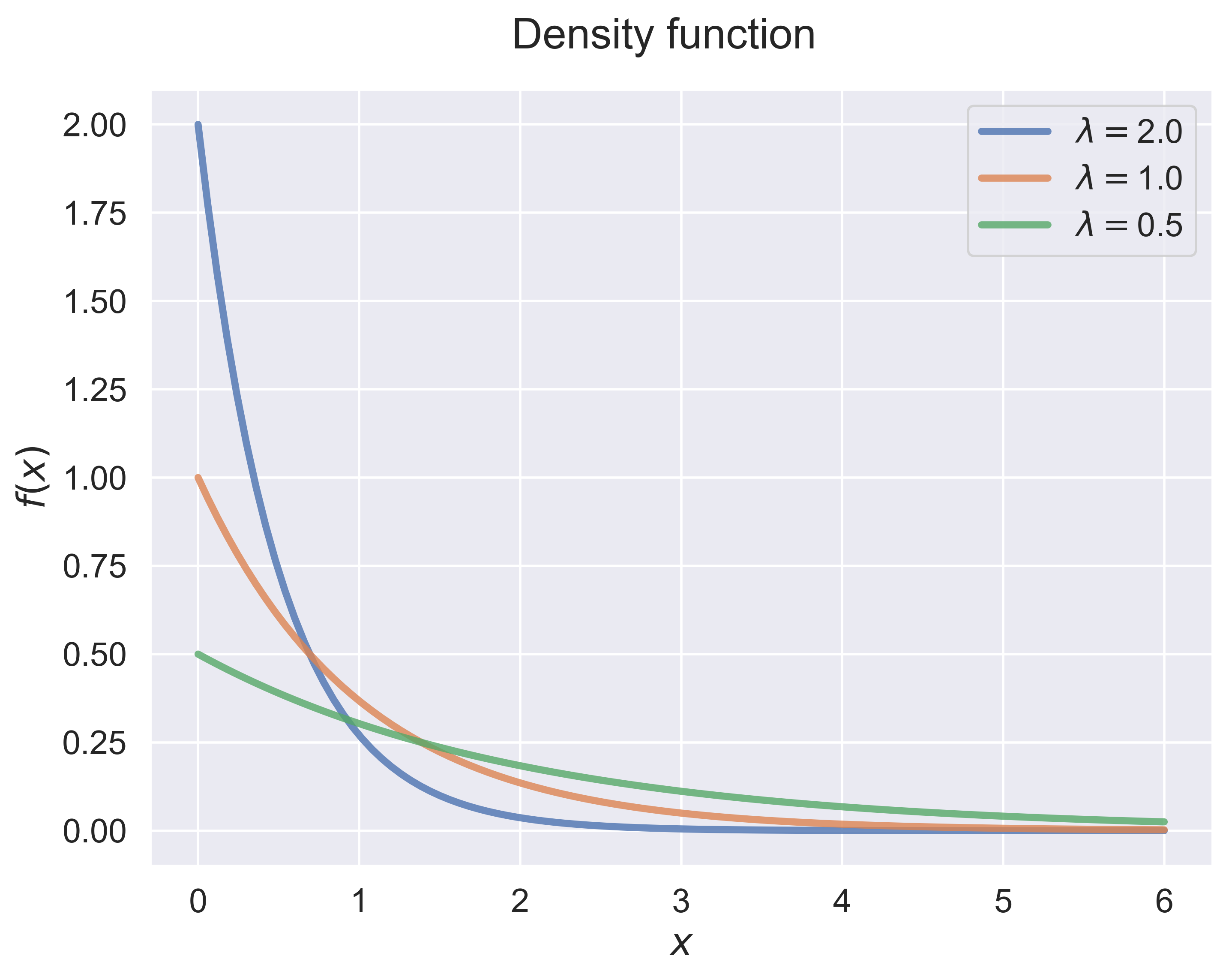
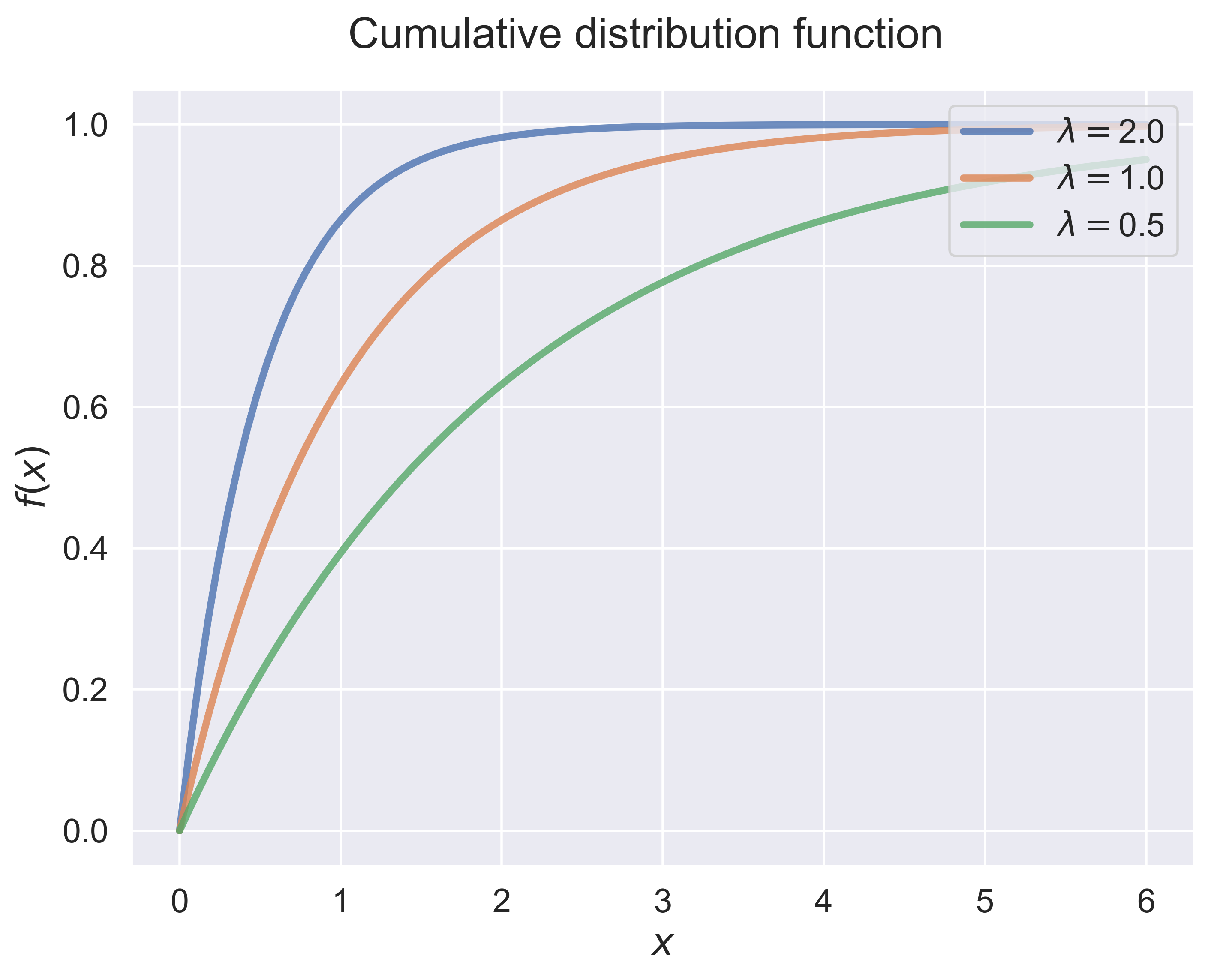
Exponential Distribution: Density Function and Cumulative Distribution Function
figure_exp_dist(job = 'pdf', fsize = (8, 6), fs = 18)
figure_exp_dist(job = 'cdf', fsize = (8, 6), fs = 18)
Slides 0706
-
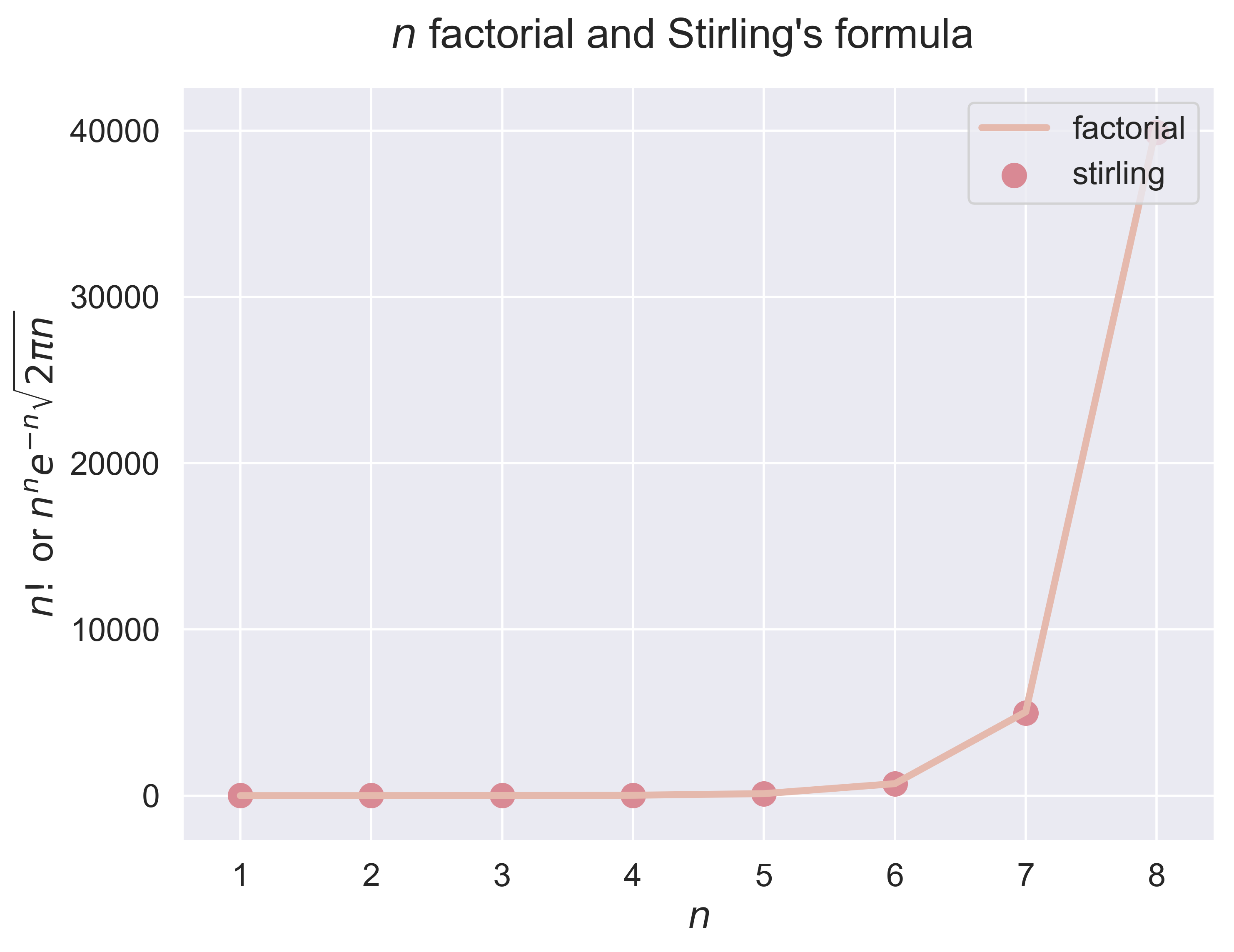
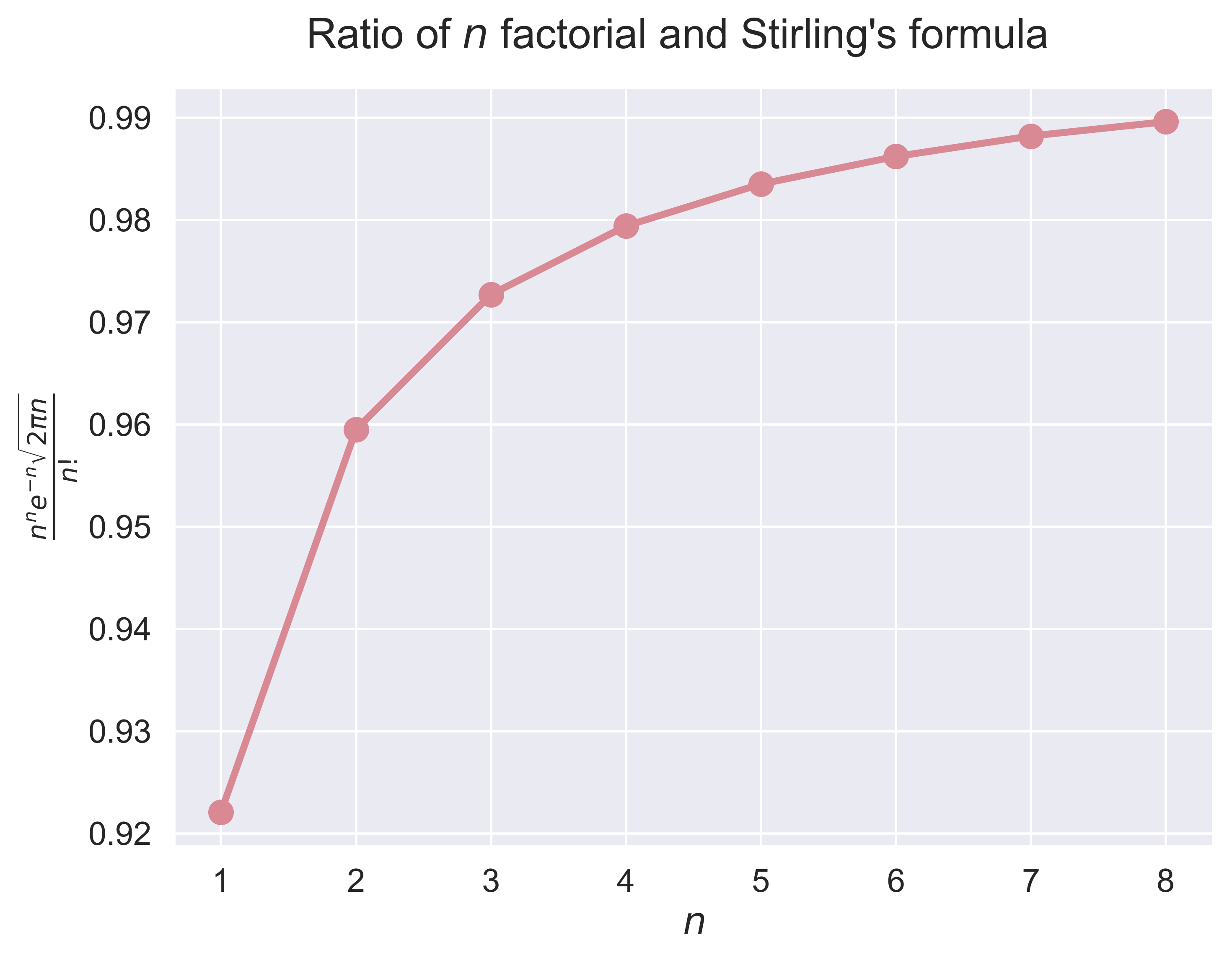
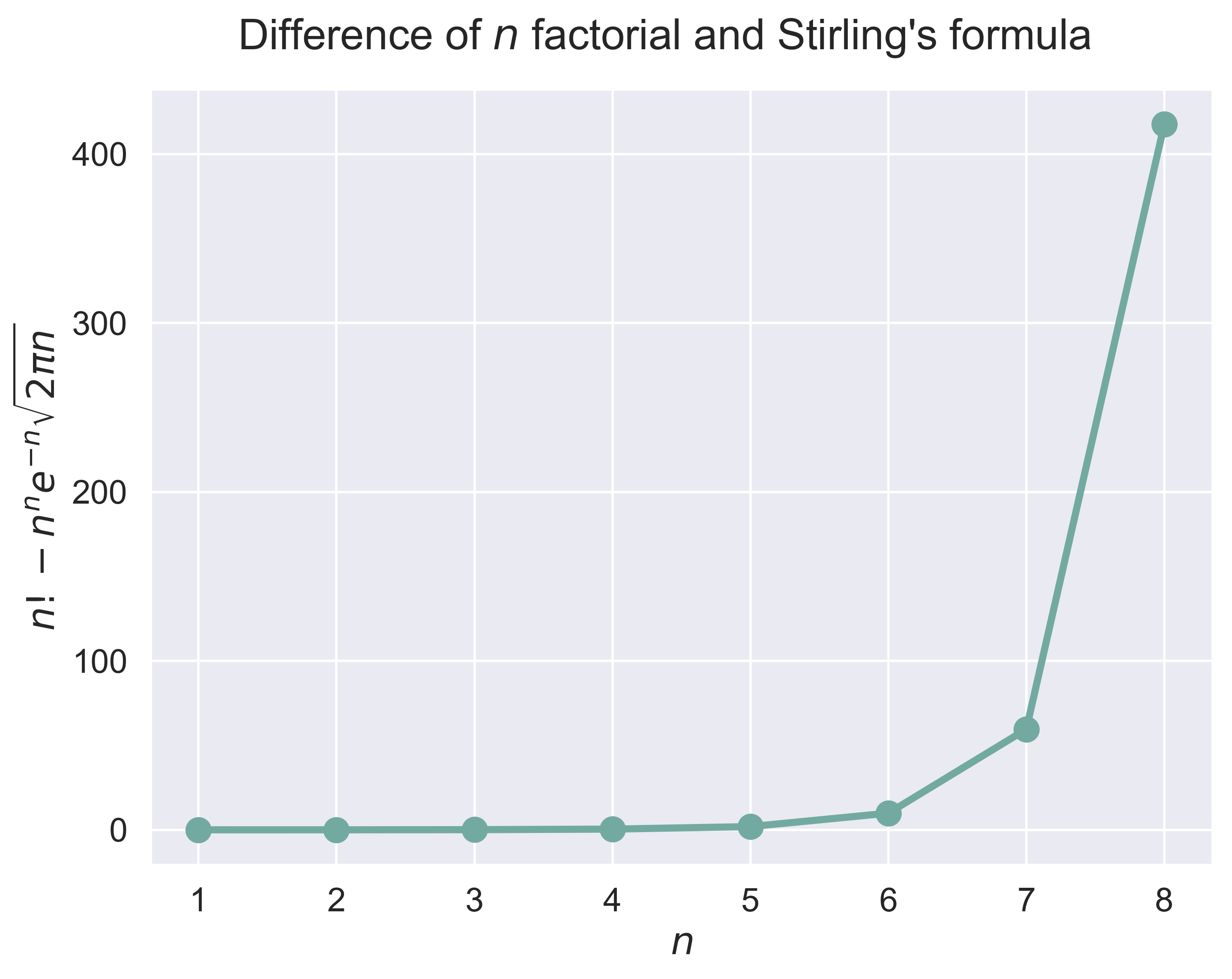
stirling(n = 10)
figure_stirling(n = 8, fsize = (8, 6), fs = 18)
-
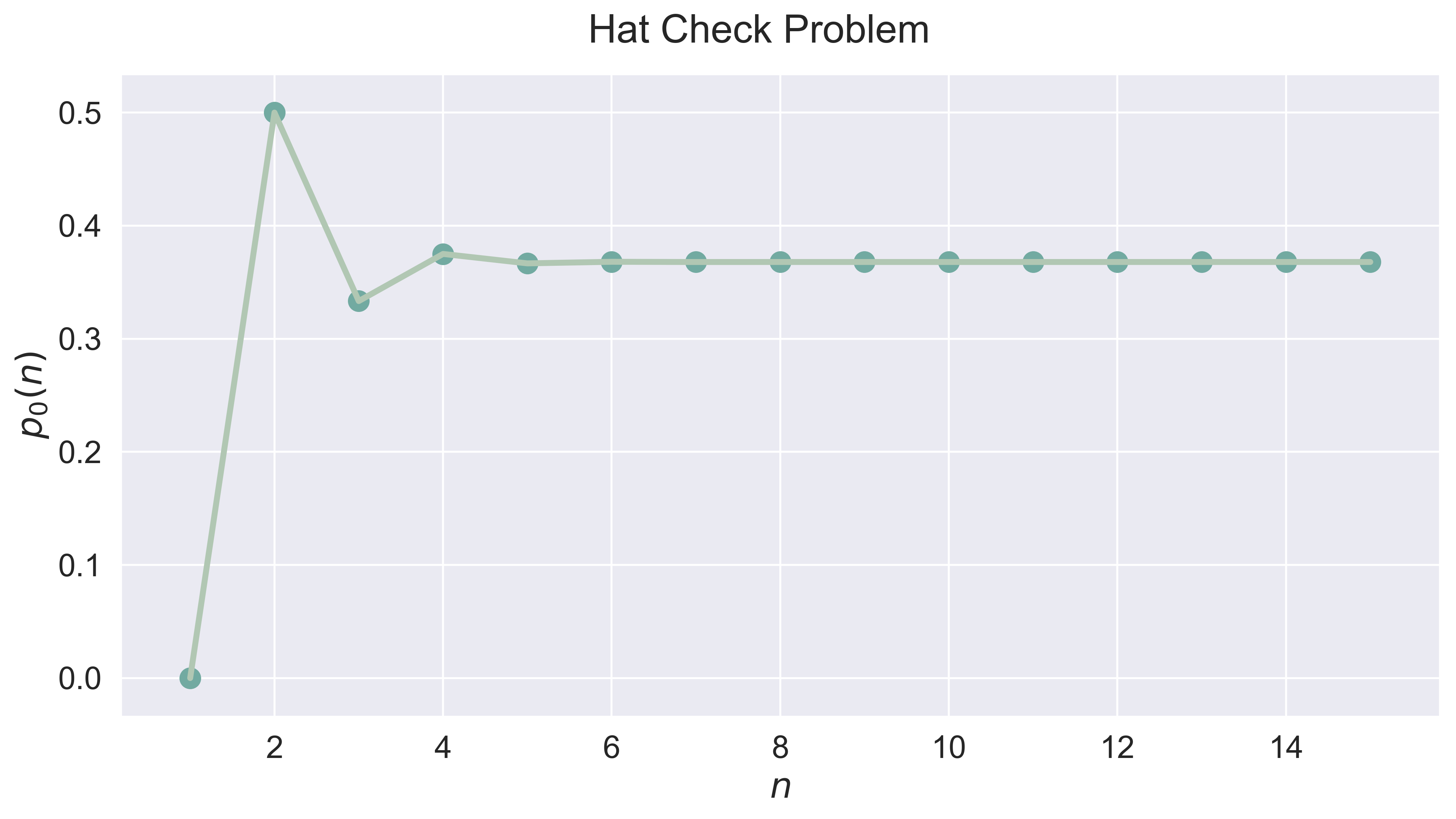
Hat Check Problem (Fixed Point)
hat_check(n = 10)
figure_hat_check(n = 15, fsize = (12, 6), fs = 20)
Slides 0708
-
Pascal’s Triangle
from scipy.special import comb
pascal(n = 10, j = 5)
Quiz 4
-
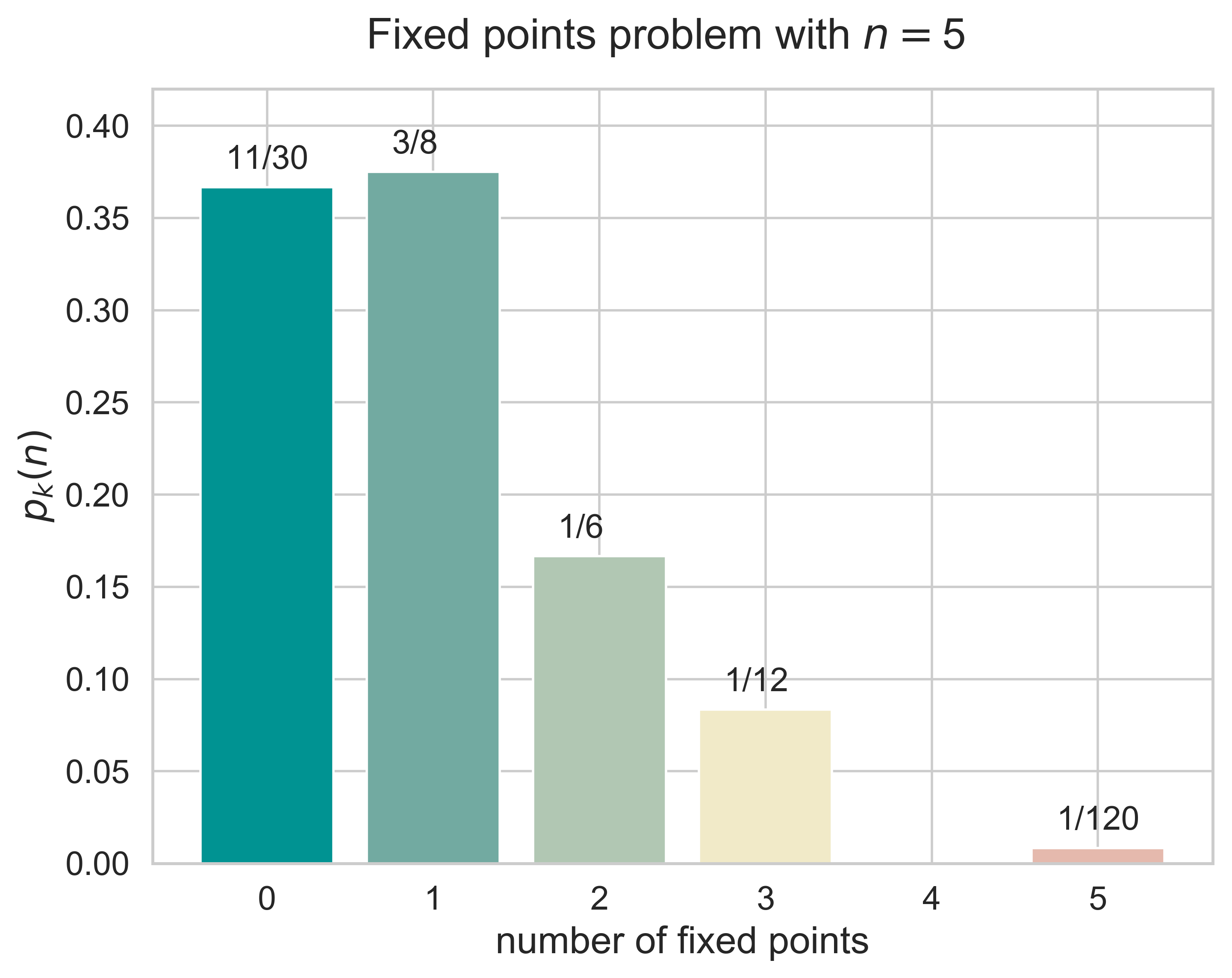
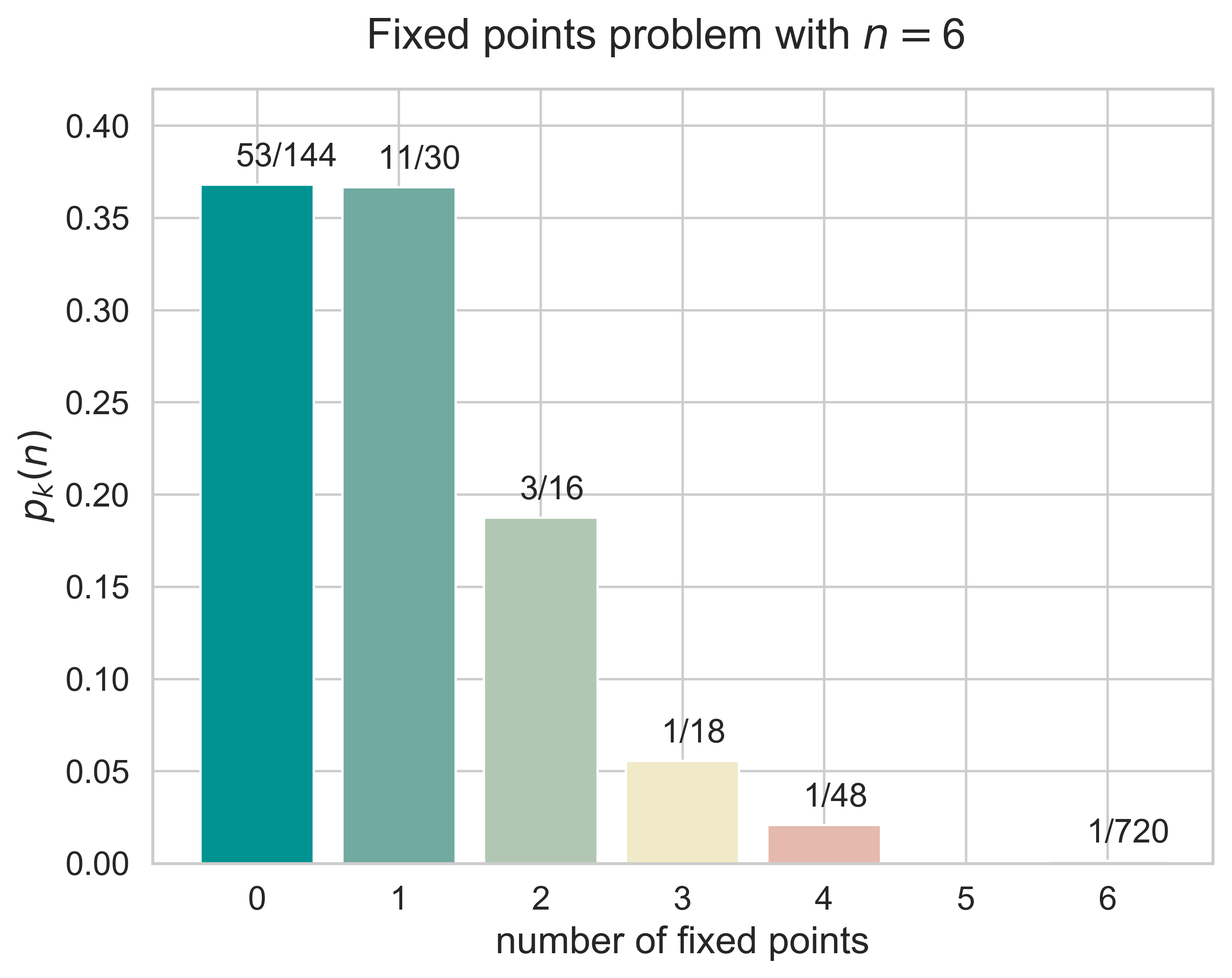
Fixed Points
fixed_points(n = 6, printing = True)
figure_fixed_points(n = 6, fsize = (8, 6), fs = 18)
Slides 0710
-
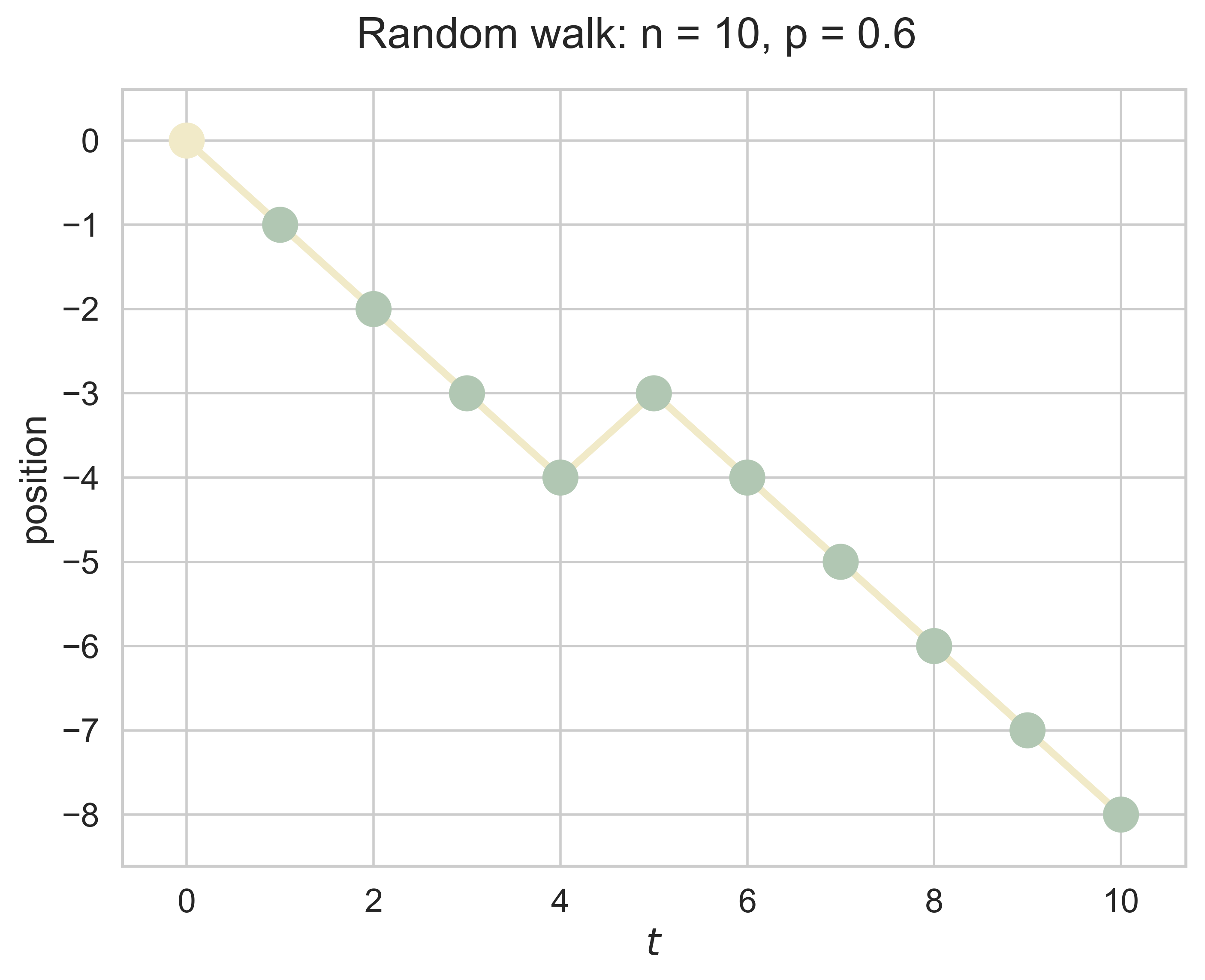
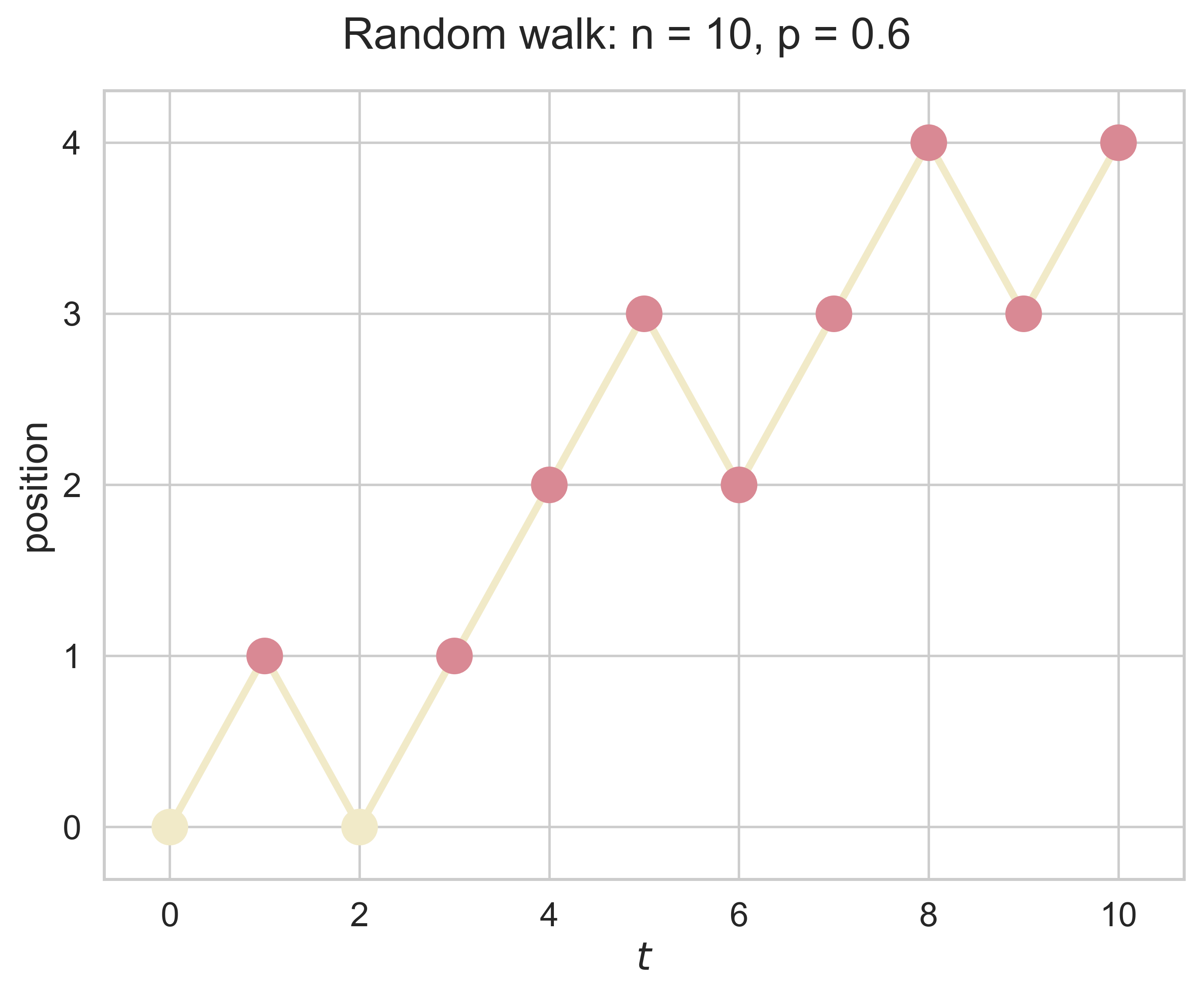
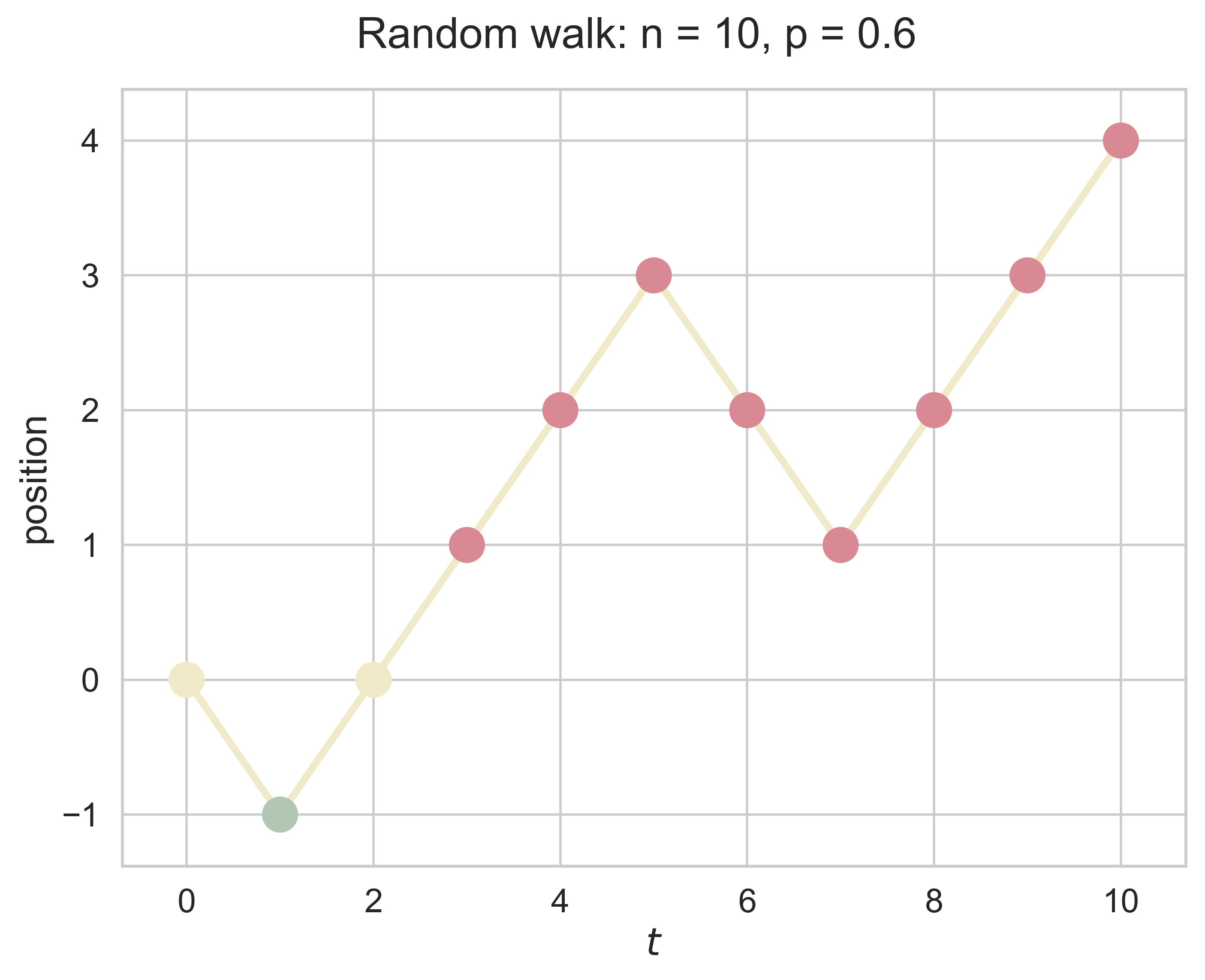
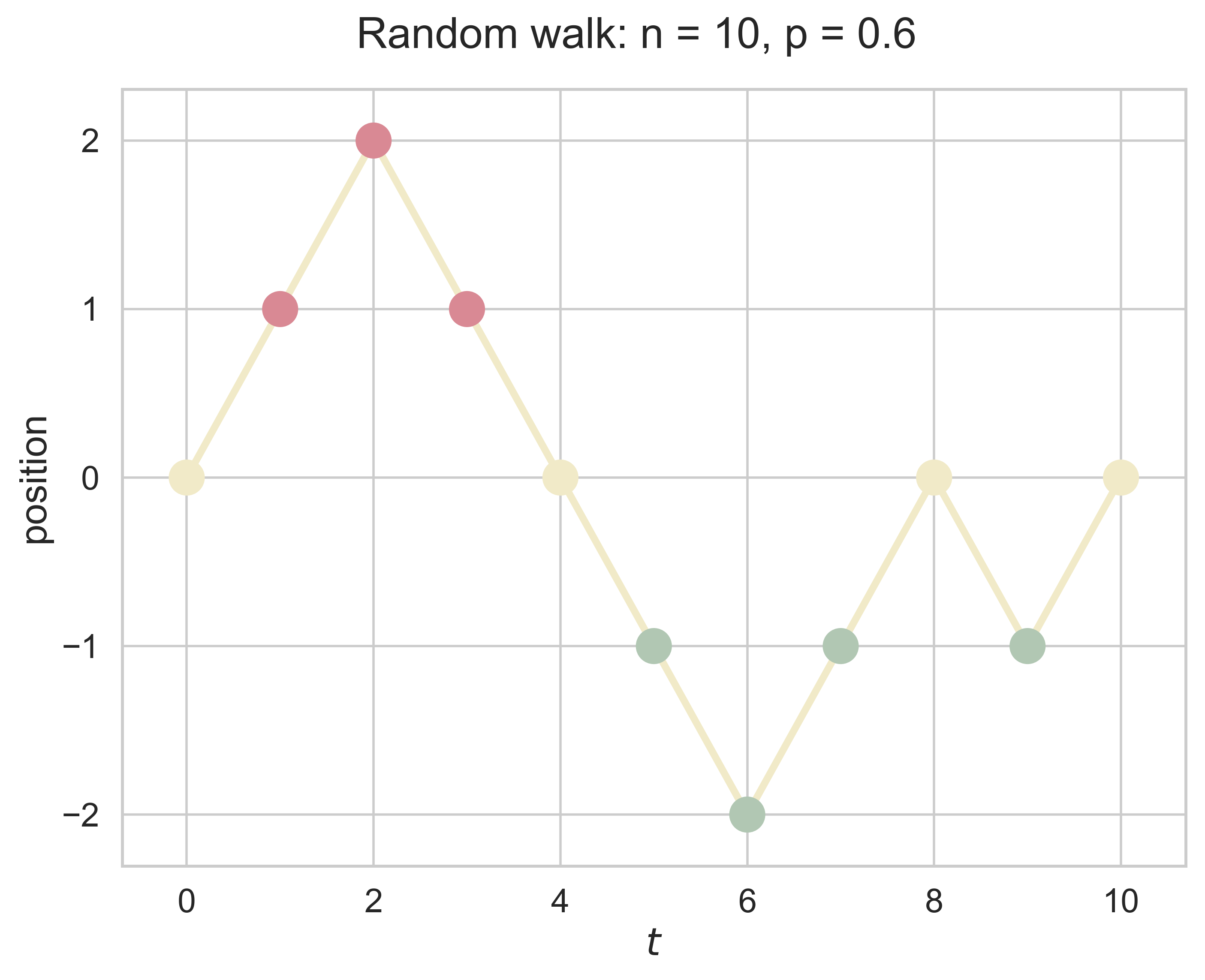
One Dimensional Random Walk
random_walk_1D(n = 10, p = 0.6)
path_rw_2D(n = 10, p = 0.6, fsize = (8, 6), fs = 18, index = 1)
-
Two Dimensional Random Walk: A Homework Problem
-
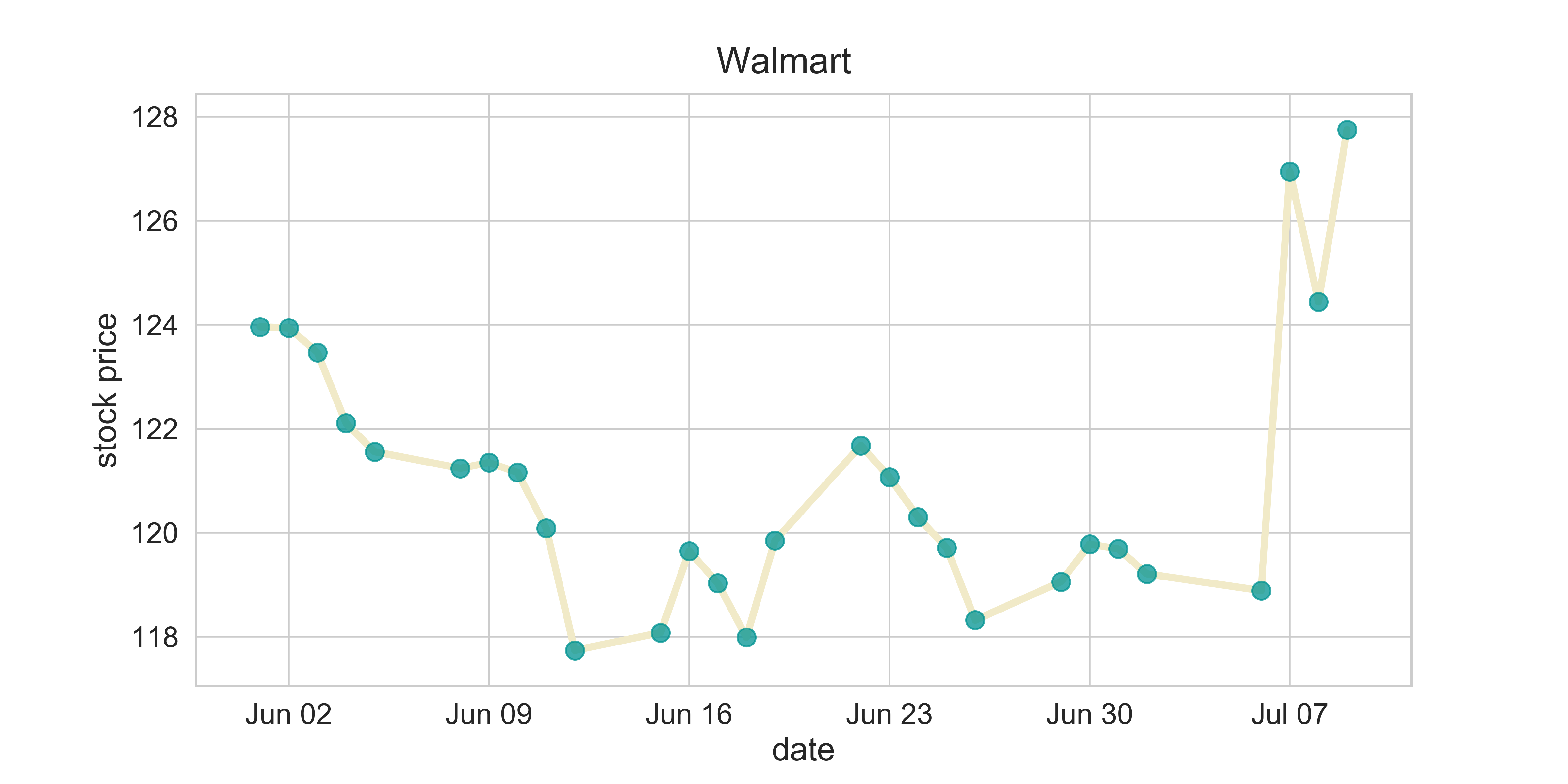
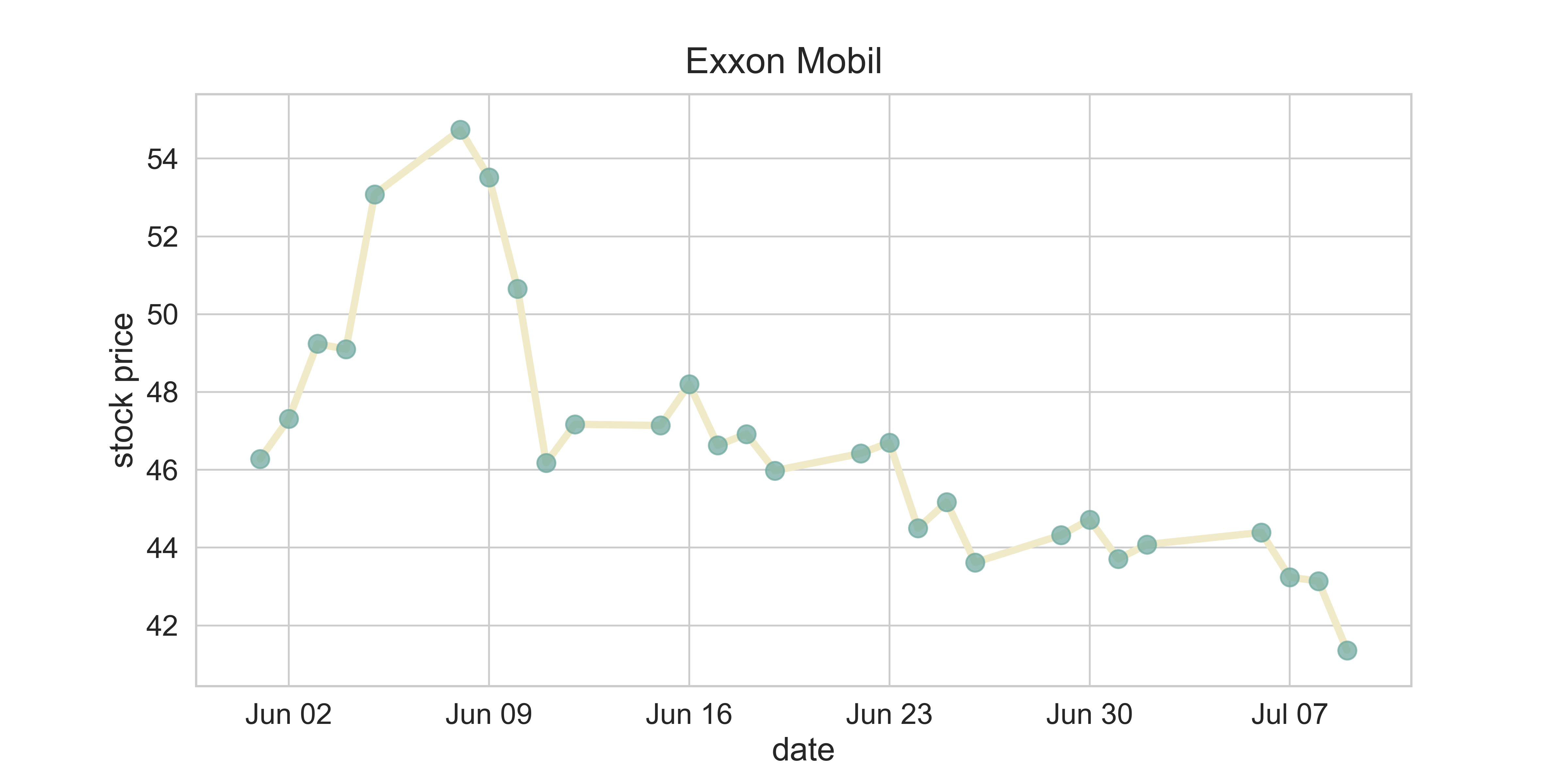
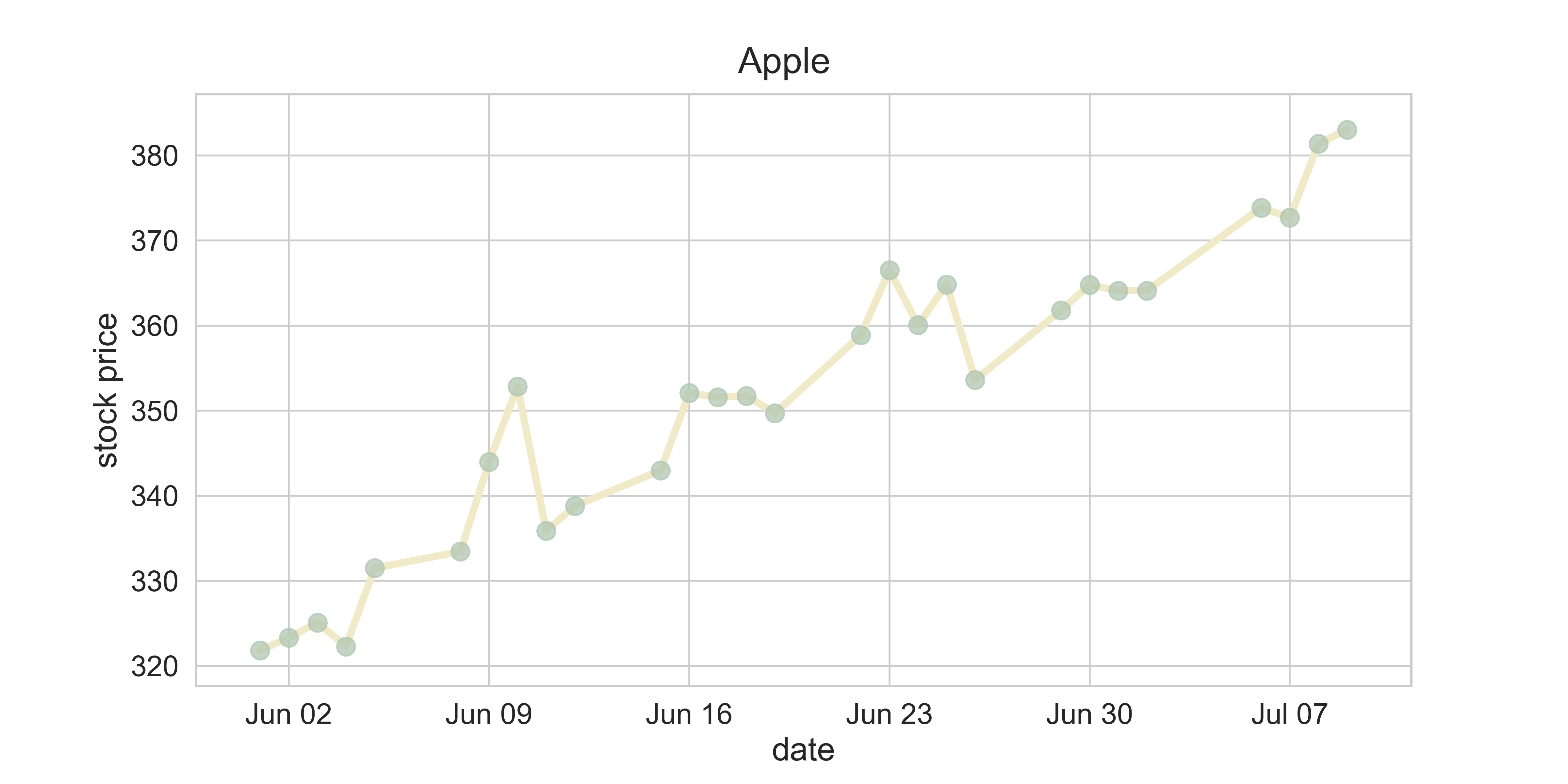
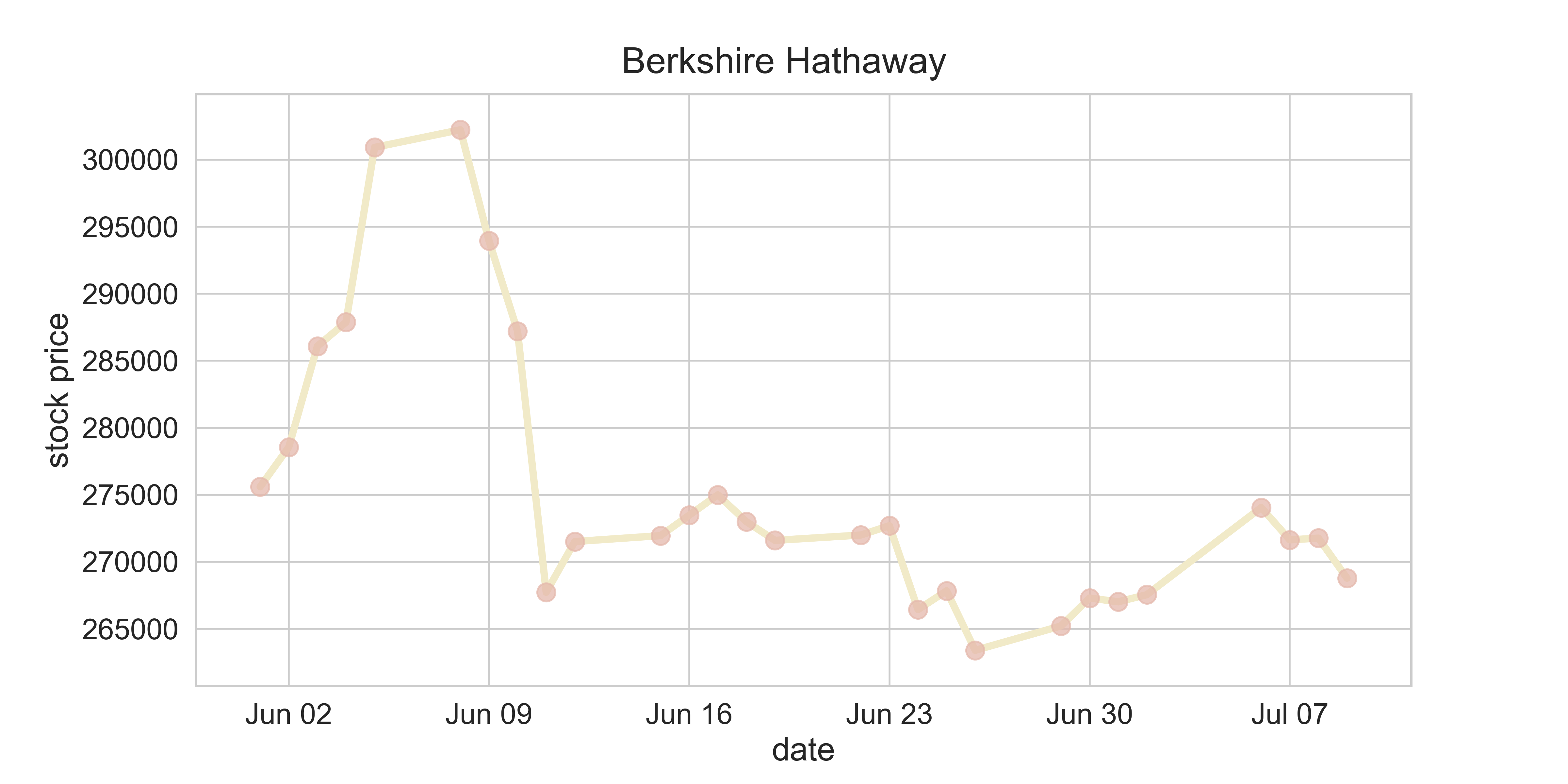
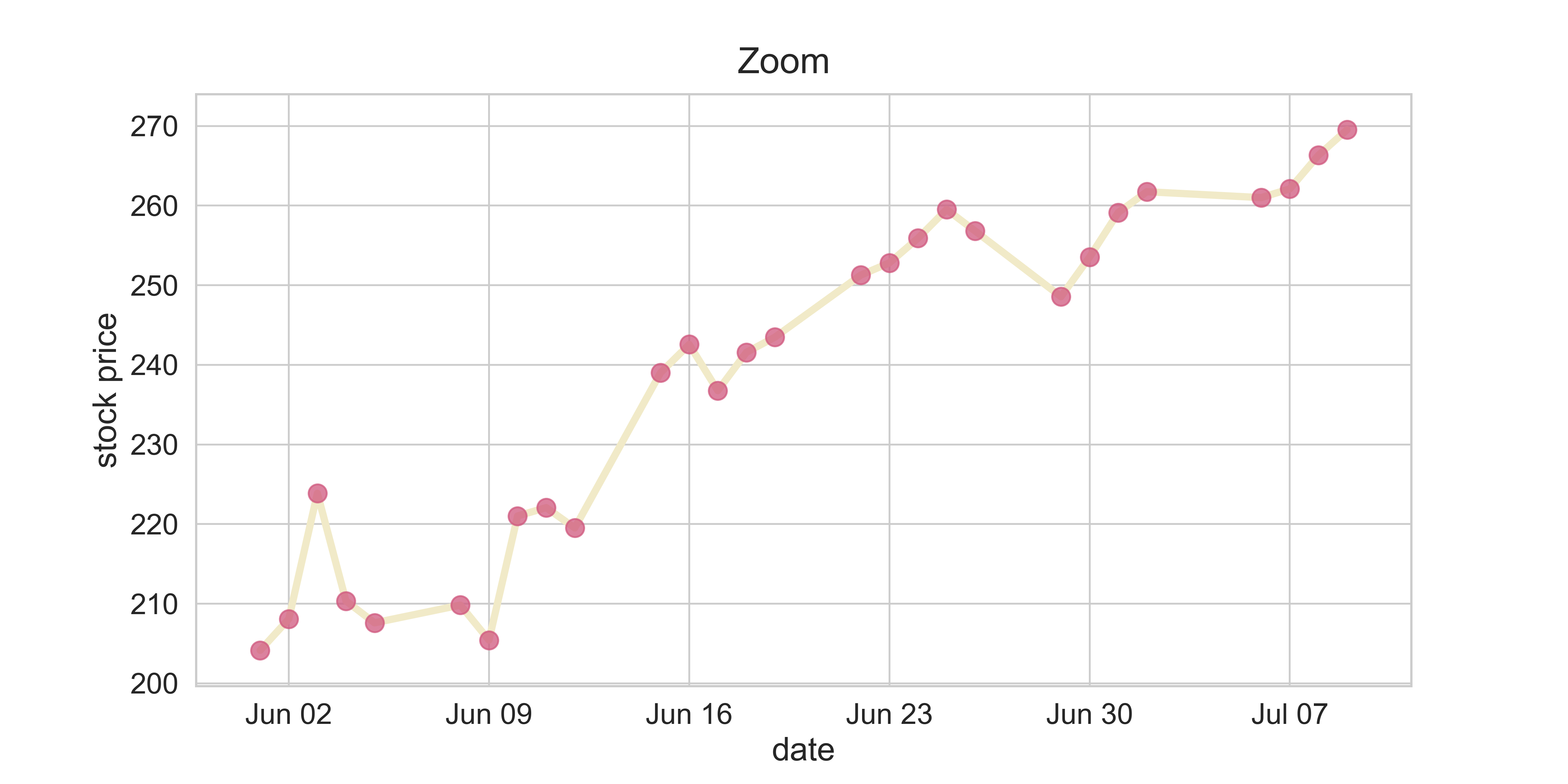
Stock Market
import yfinance as yf
load_STOCK_raw(company_index = 'AAPL')
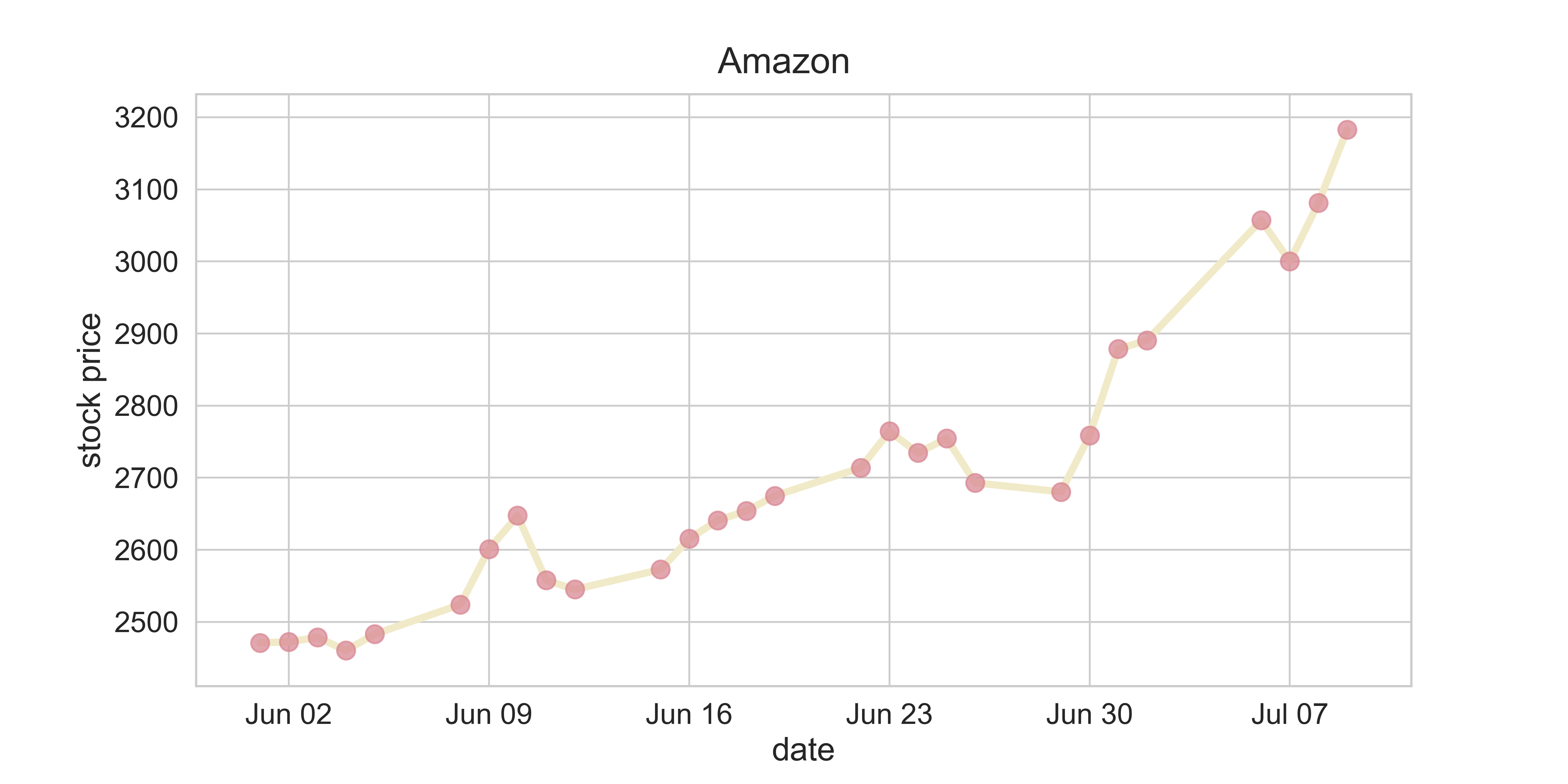
figure_stock_price(company_index = 'AMZN', date_initial = datetime.date(int(2020),int(6),int(1)),
fsize = (12, 6), fs = 20)
-
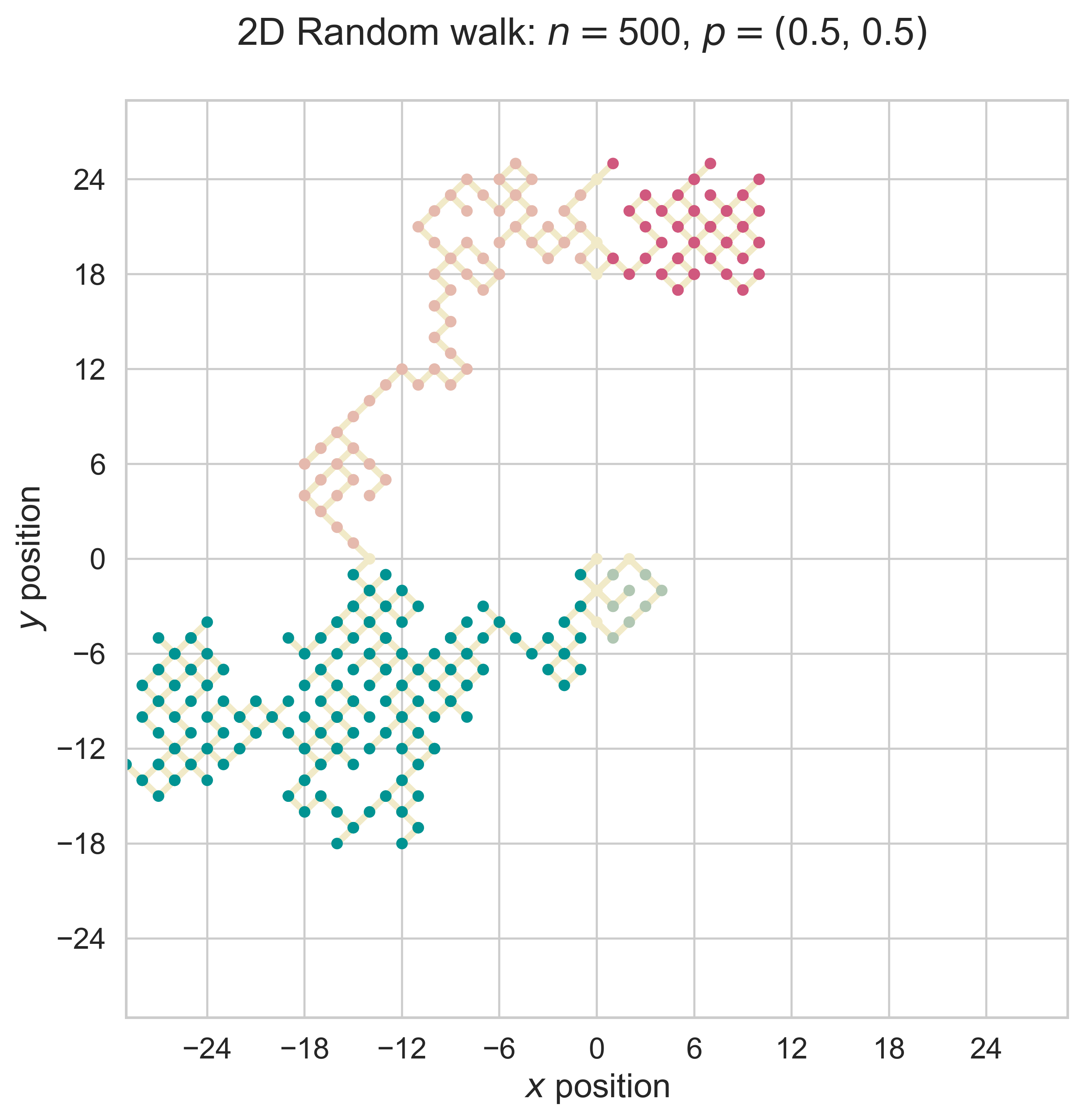
Two Dimensional Random Walk (Take-Home Problem)
random_walk_2D(n = 500, p_x = 0.5, p_y = 0.5)
path_rw_2D(n = 500, p_x = 0.5, p_y = 0.5, fsize = (8, 8), fs = 18, index = 1)
Slides 0717
-
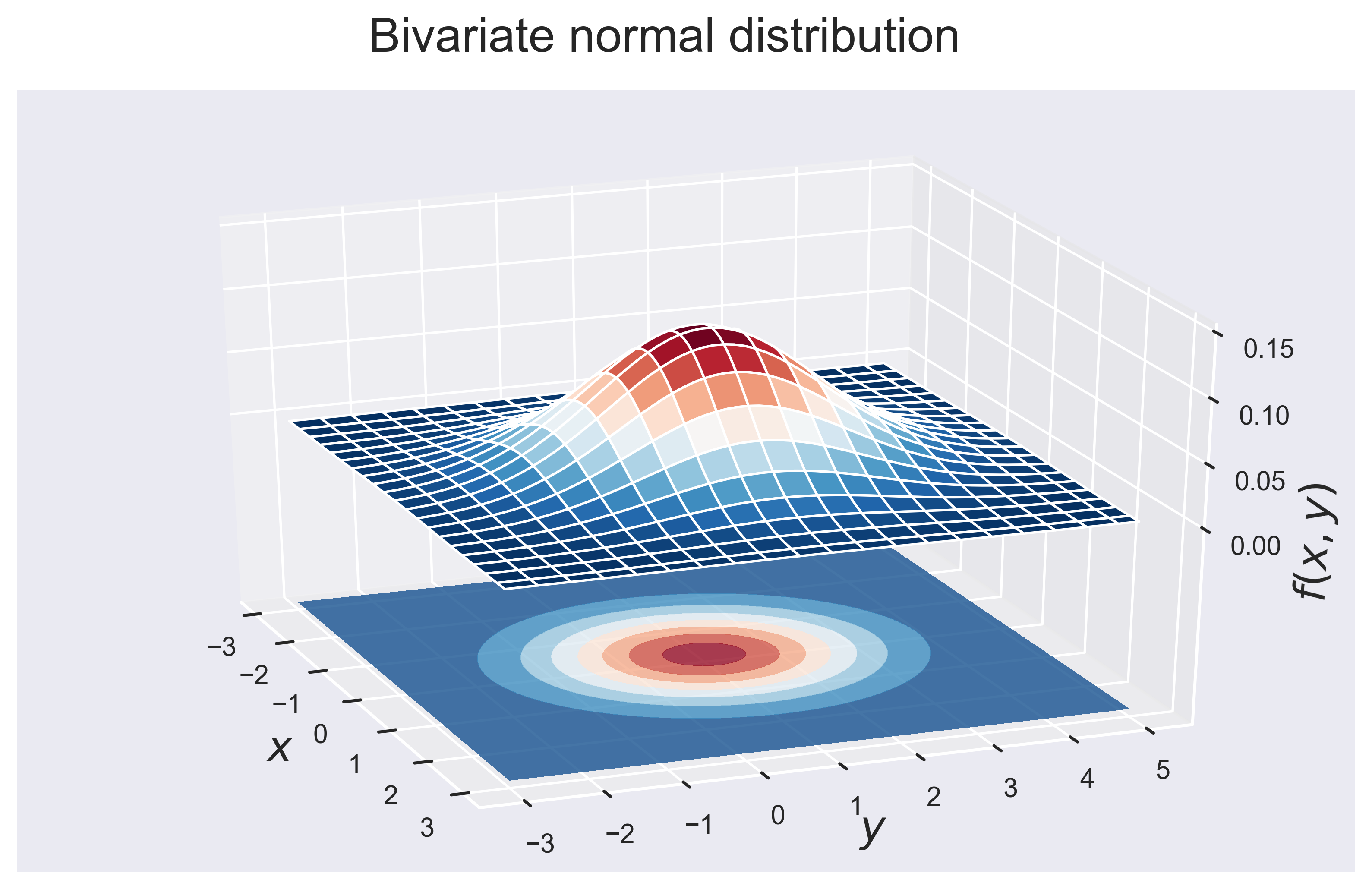
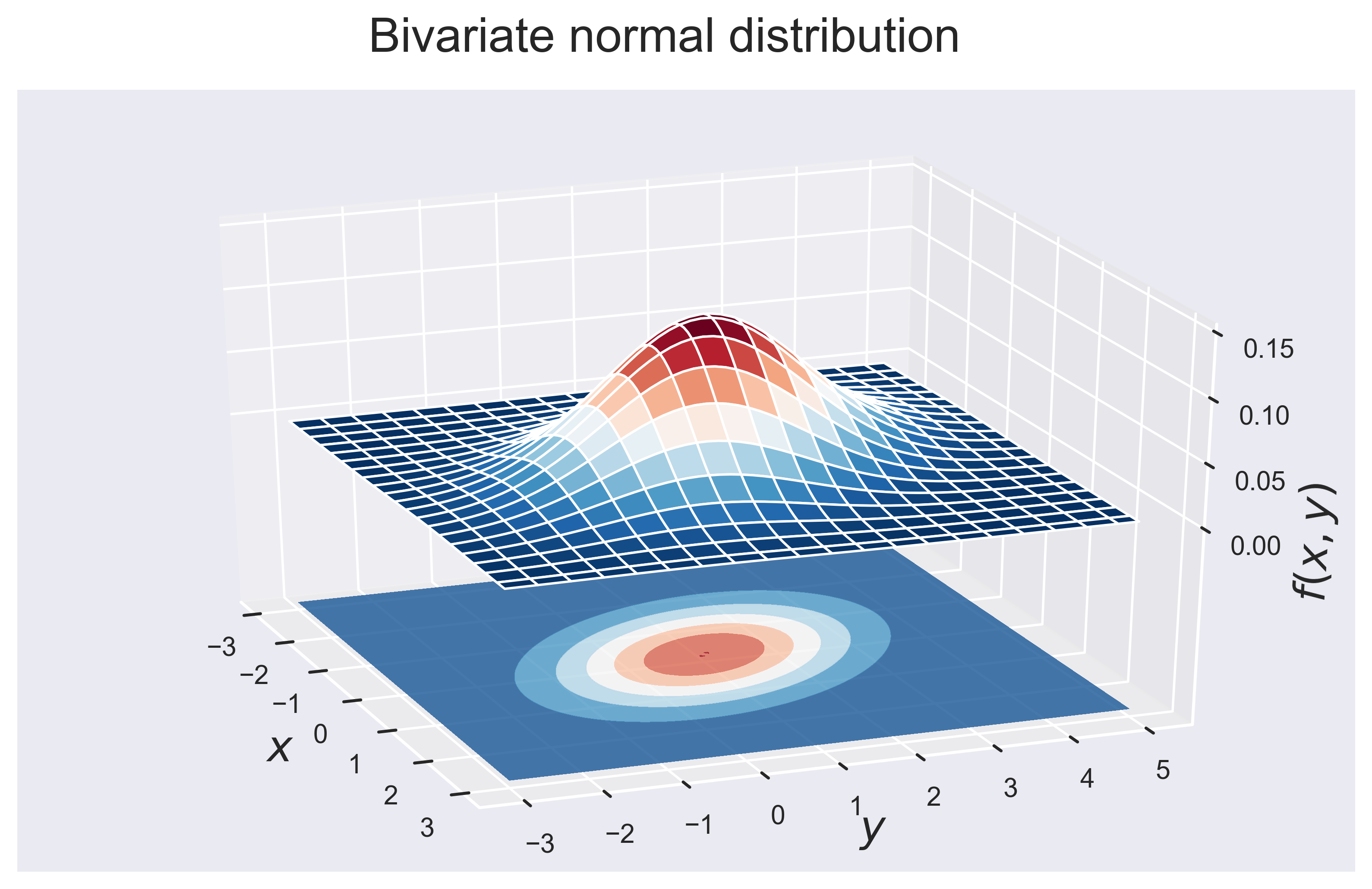
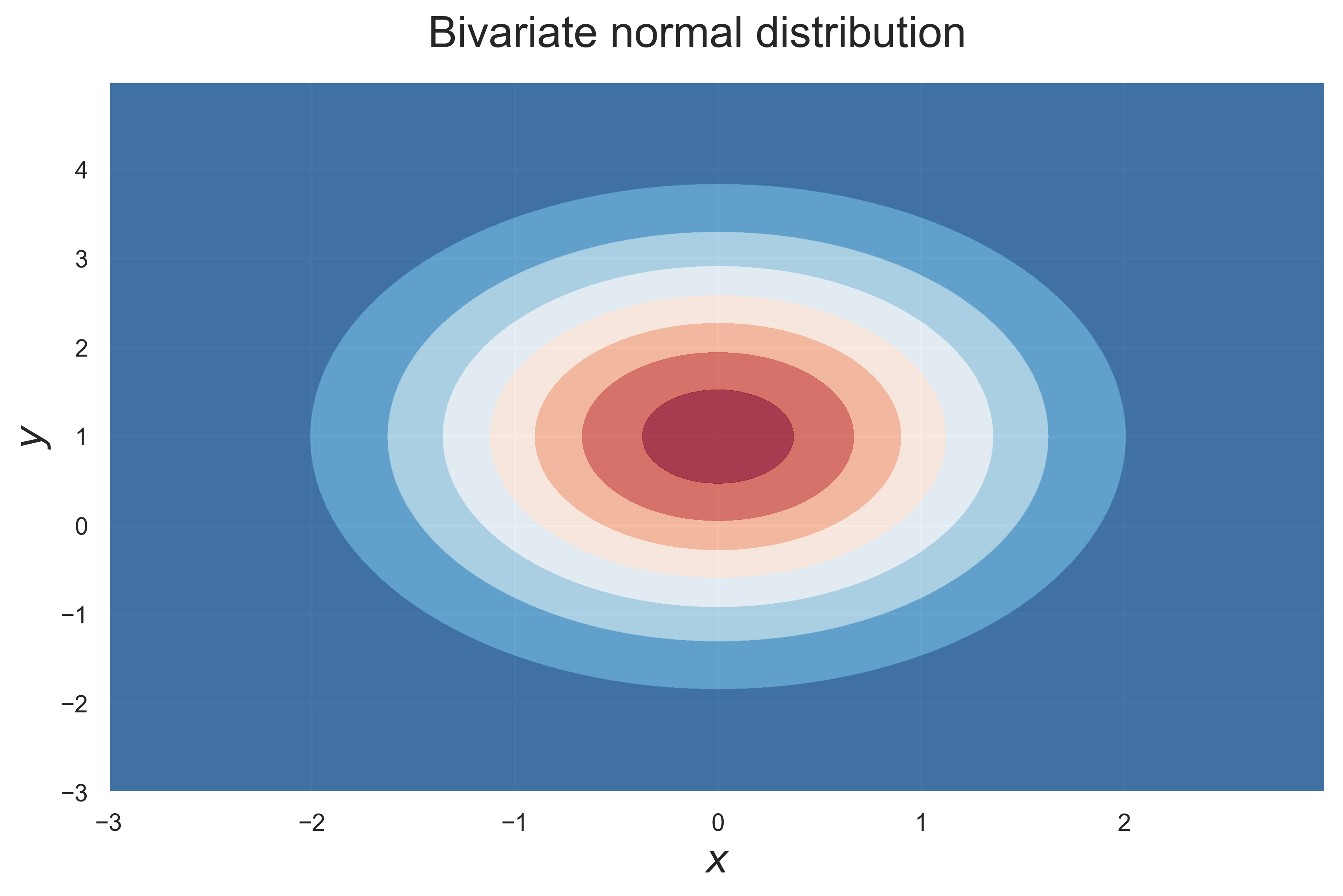
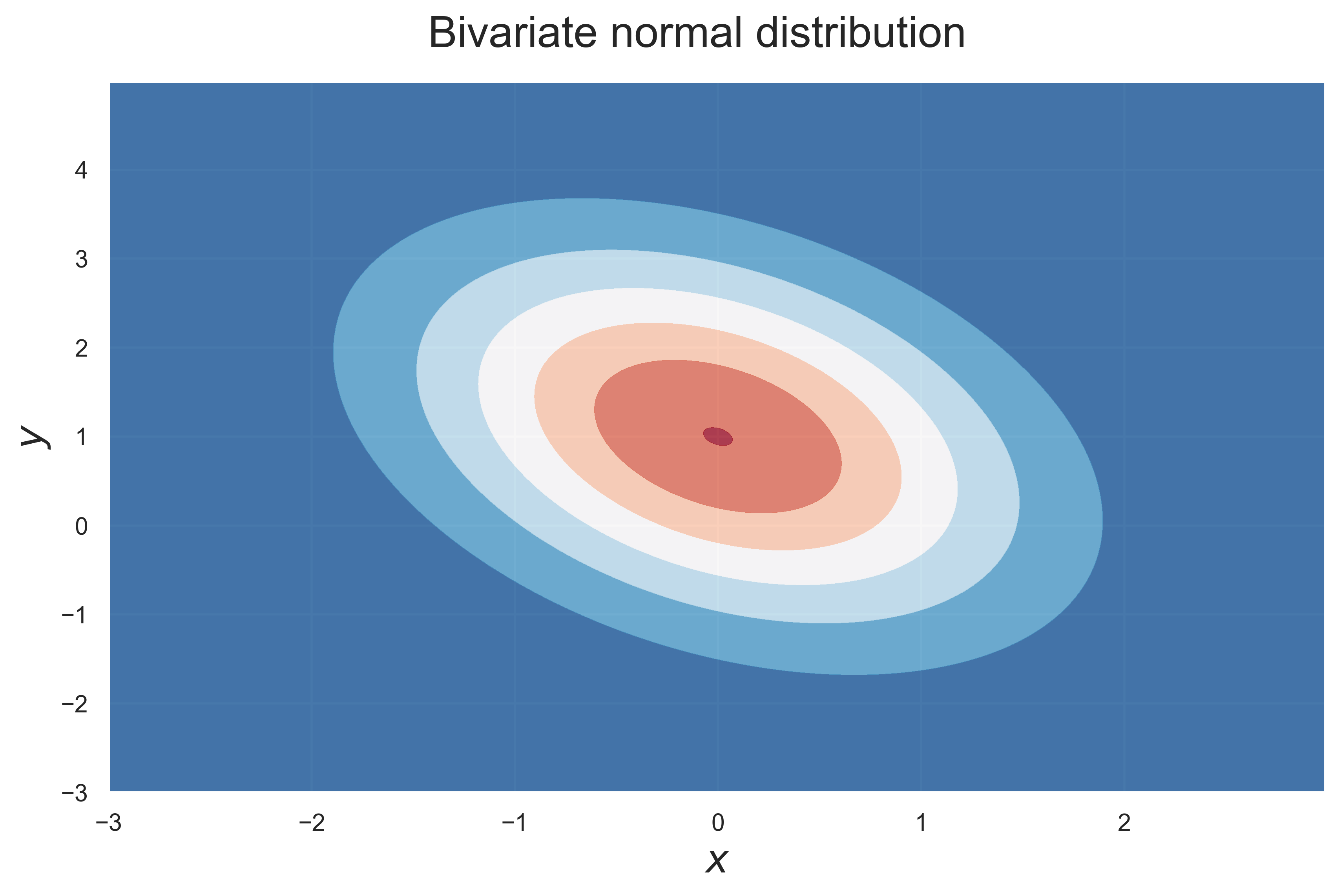
Two Dimensional Normal Distribution: Density Function and Contour curve
figure_normal_2d(ind = True, fsize = (10, 6), fs = 20)
figure_contour_normal_2d(ind = True, fsize = (10, 6), fs = 20)
Midterm 1
-
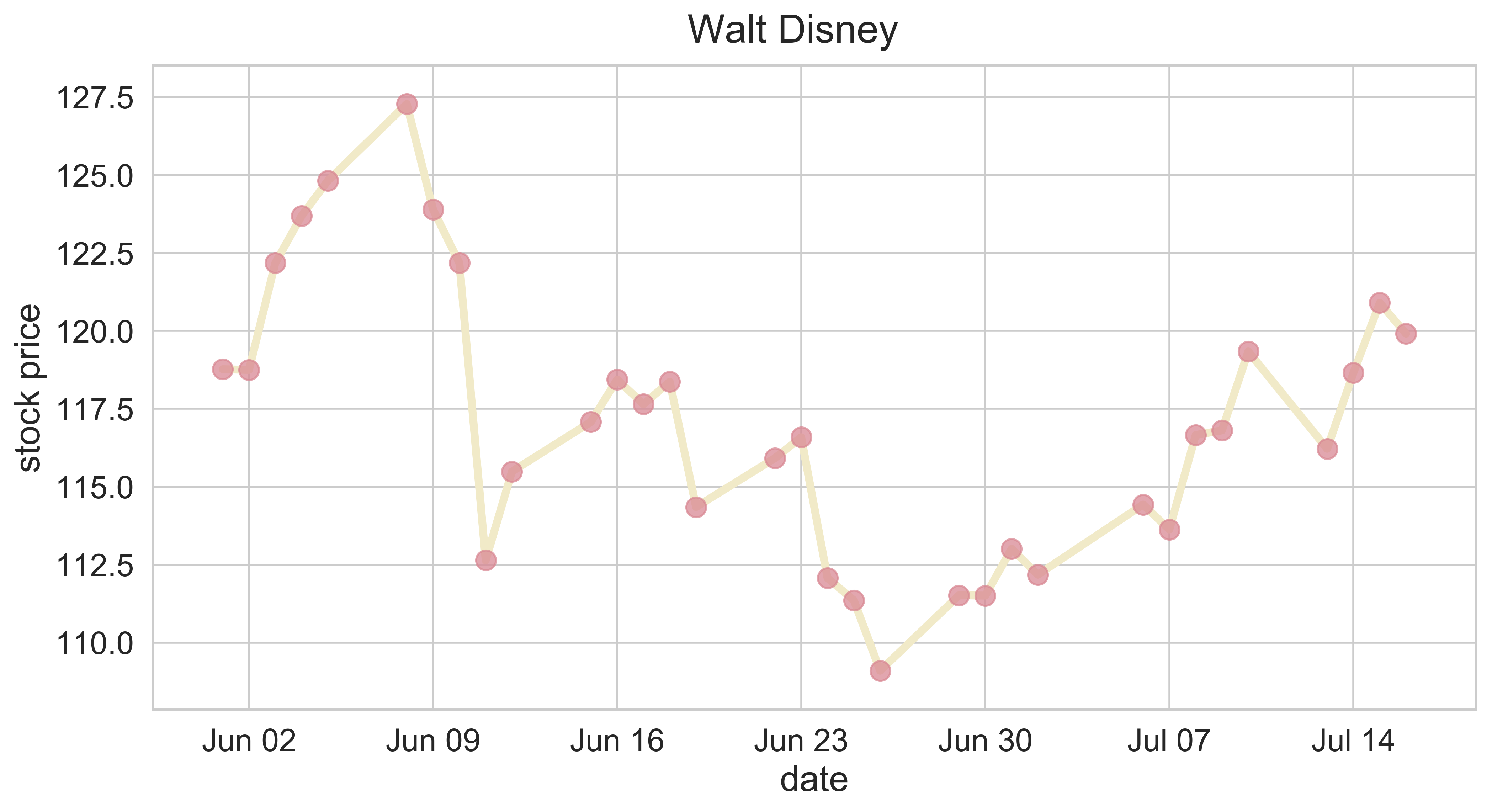
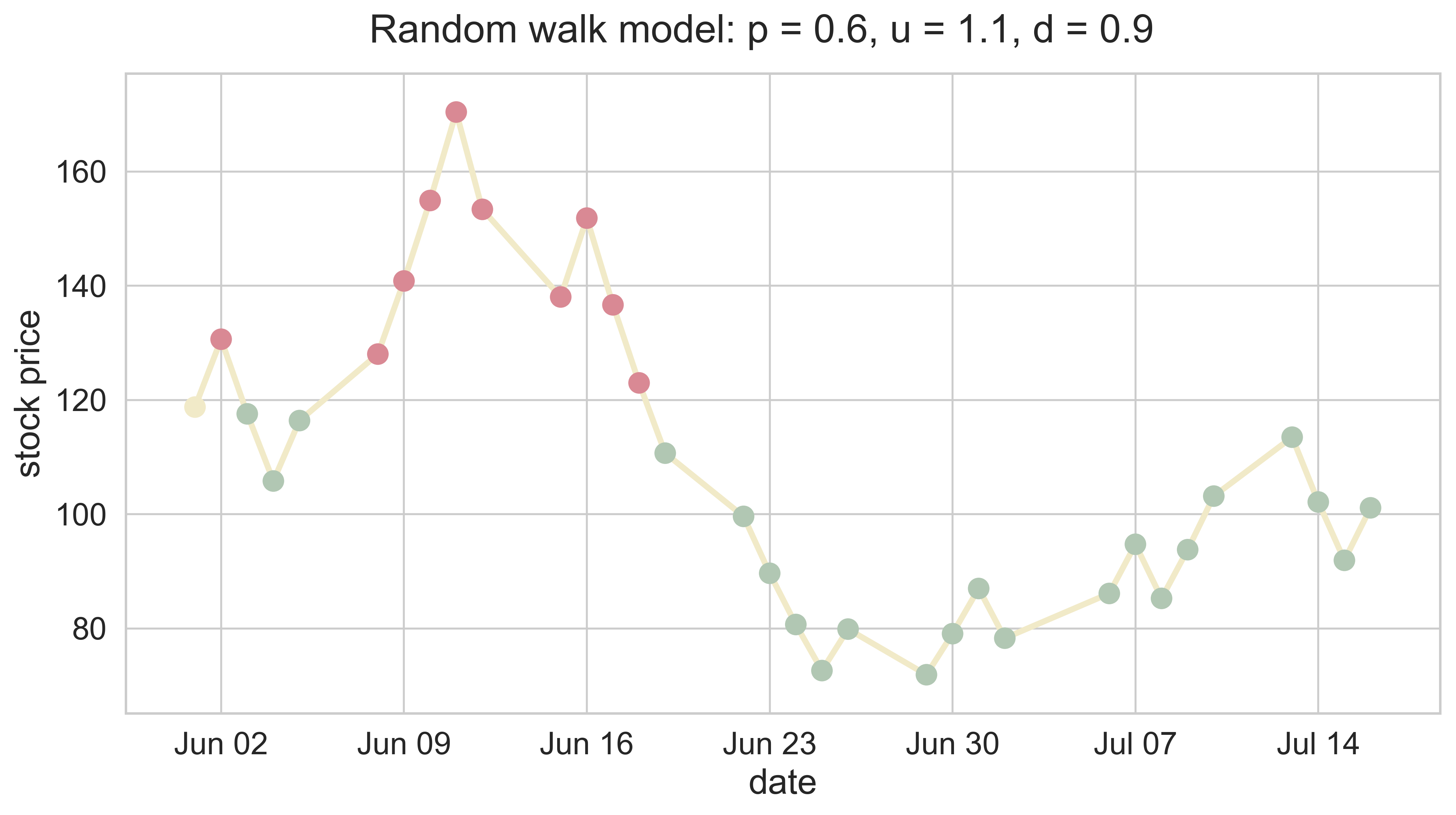
Random Walk Model for Stock Price
random_walk_sp(n = 30, p = 0.6, c = 100, u = 1.1, d = 0.9)
path_rw_sp(company_index = 'DIS', date_initial = datetime.date(int(2020),int(6),int(1)), p = 0.6, u = 1.1, d = 0.9,
fsize = (12, 6), fs = 20, index = 1)
Slides 0727
-
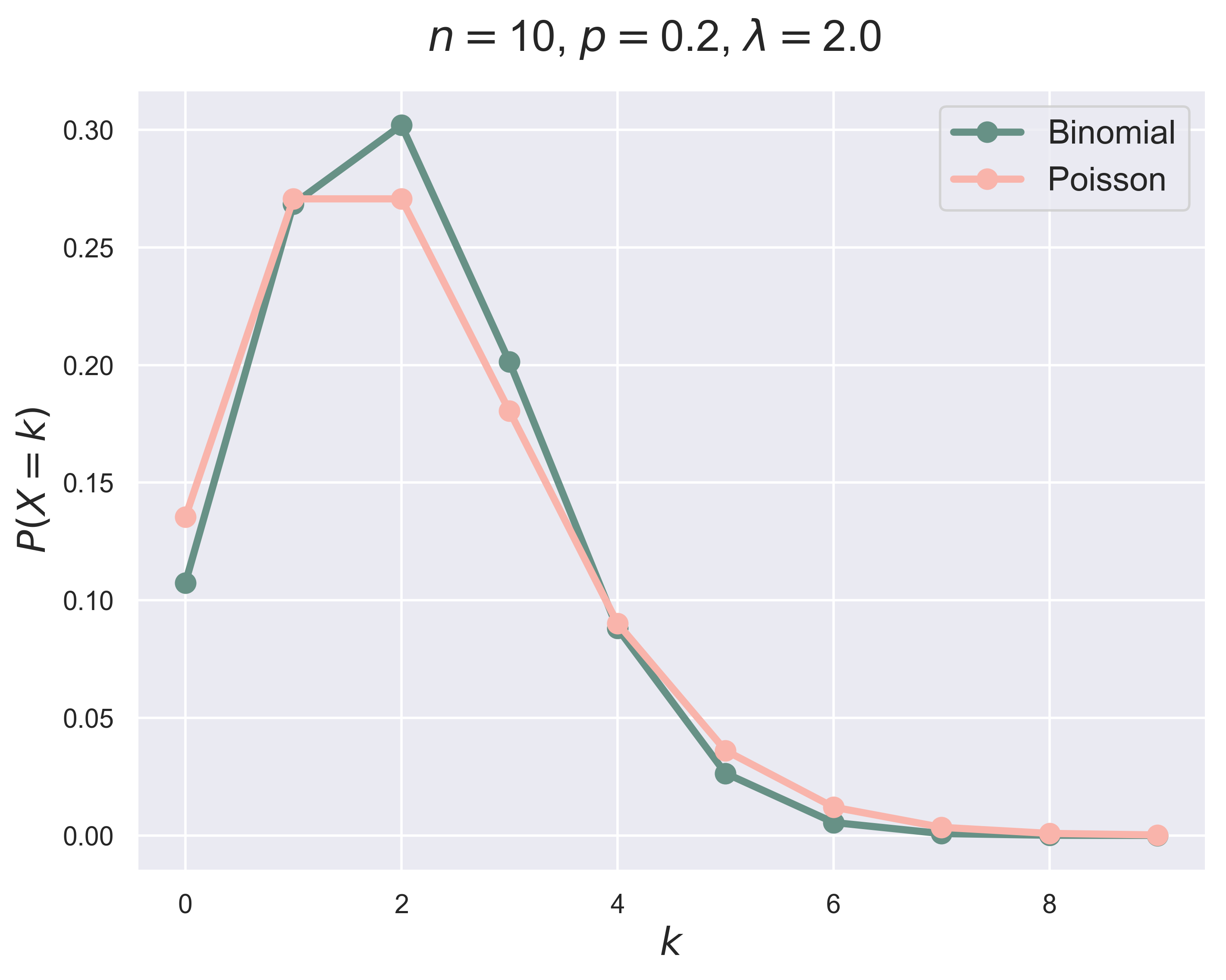
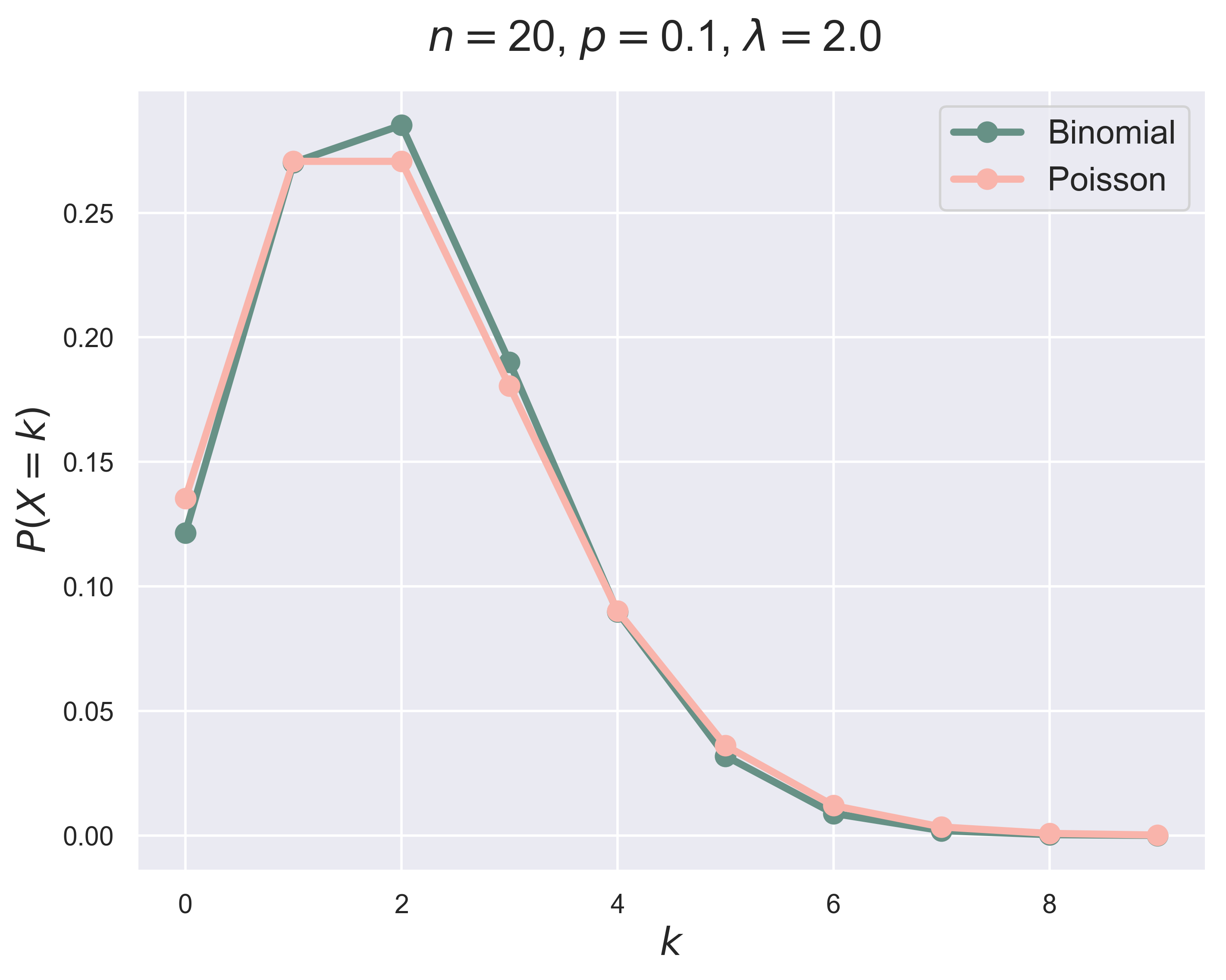
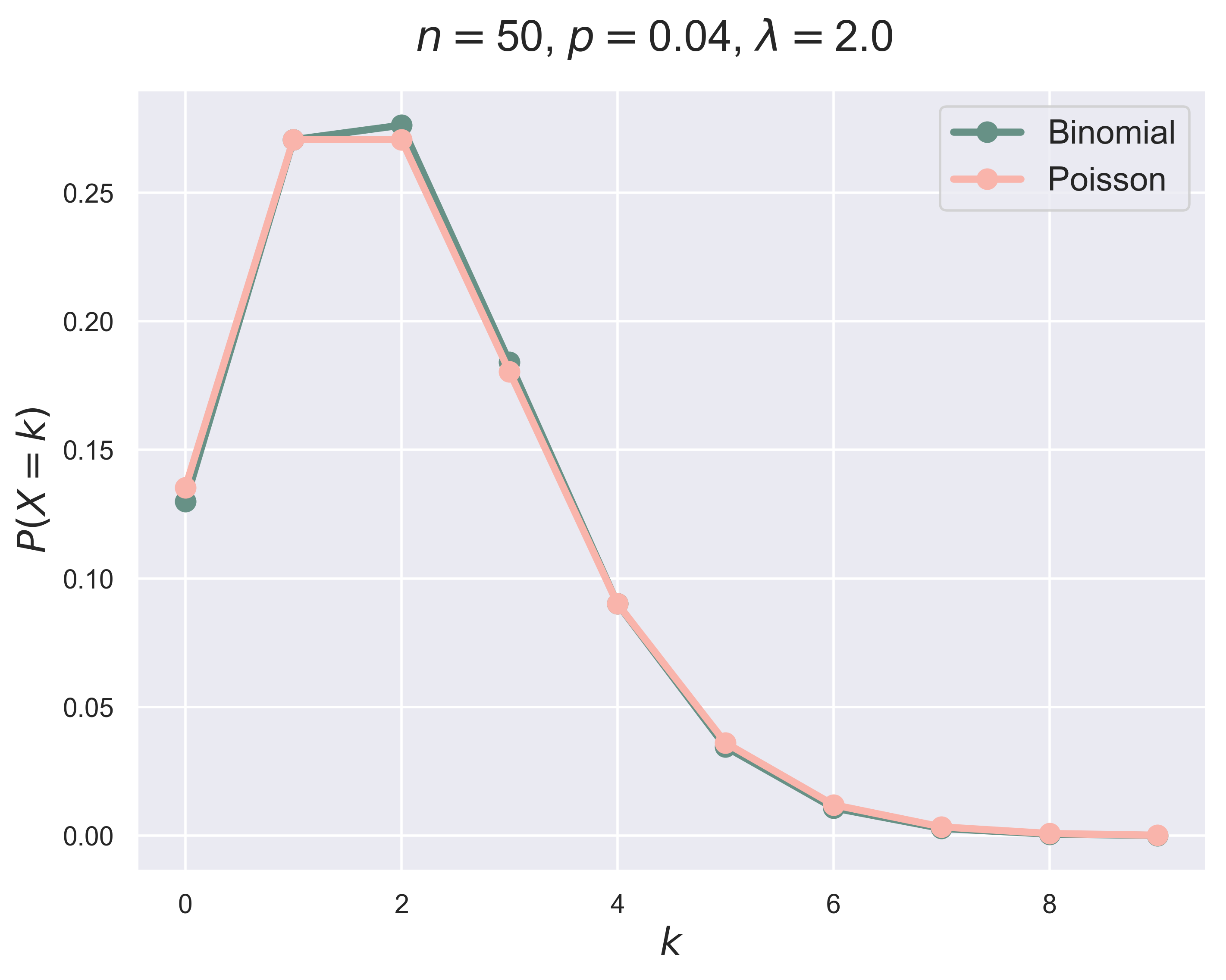
Binomial Distribution Versus Poisson Distribution
binomial_poisson_figure(n = 10, p = 0.2, fsize = (8, 6), fs = 18, tag = 1)
-
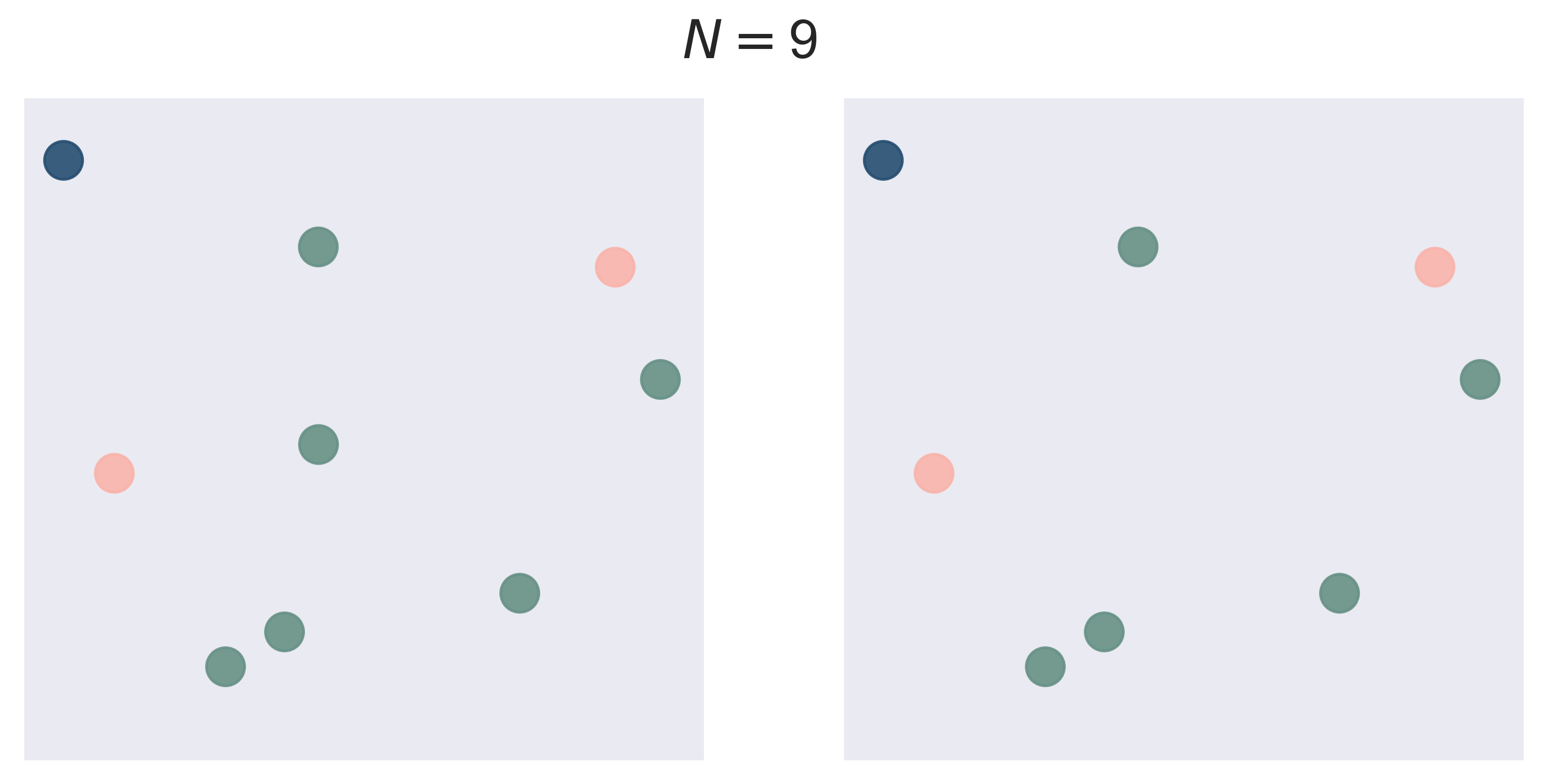
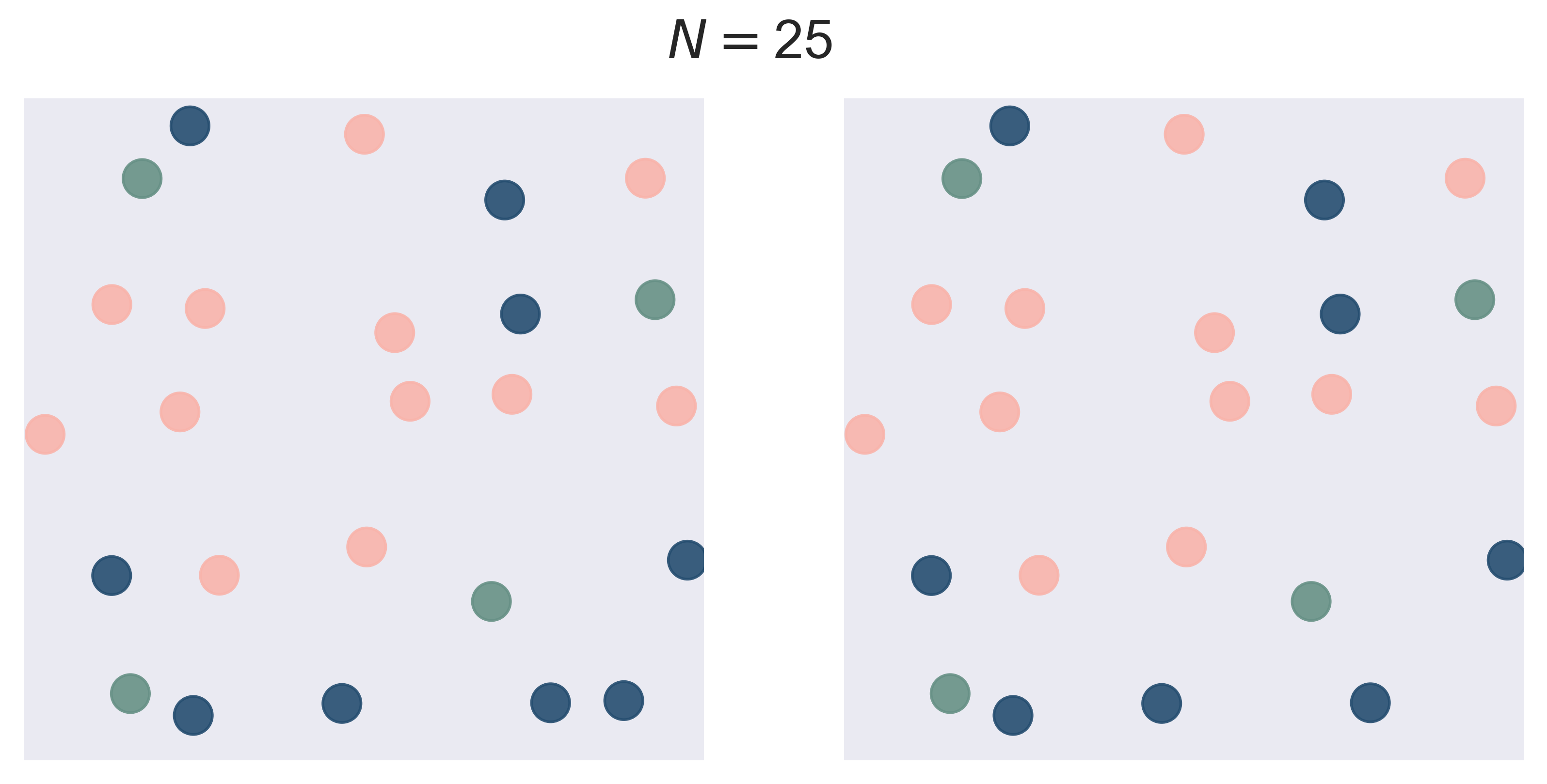
Sample With or Without Replacement
scatters(n = 3, k = 5, fsize = (10, 10), fs = 20)
Slides 0729
-
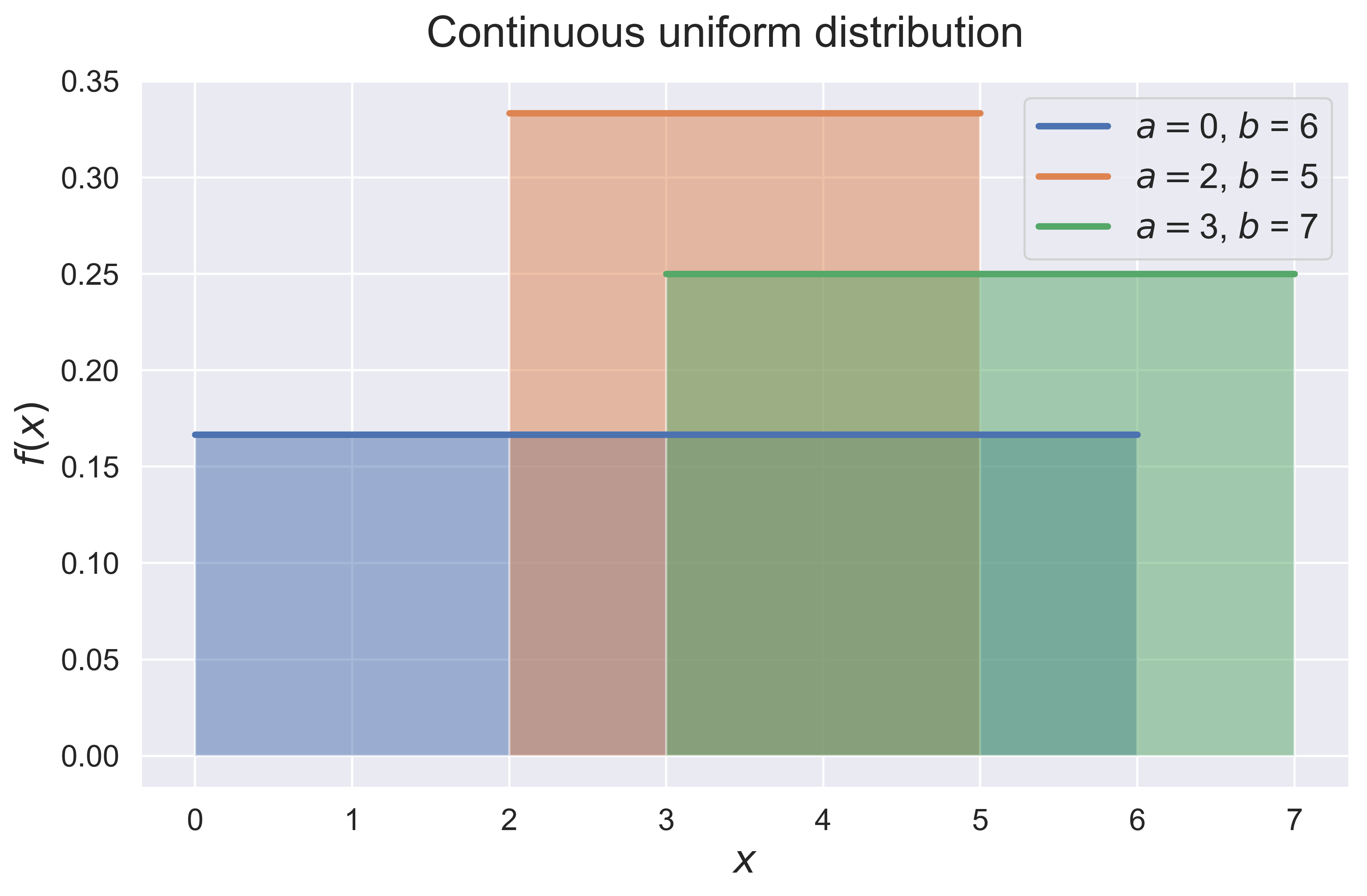
figure_continuous_uniform(fsize = (10, 6), fs = 20)
-
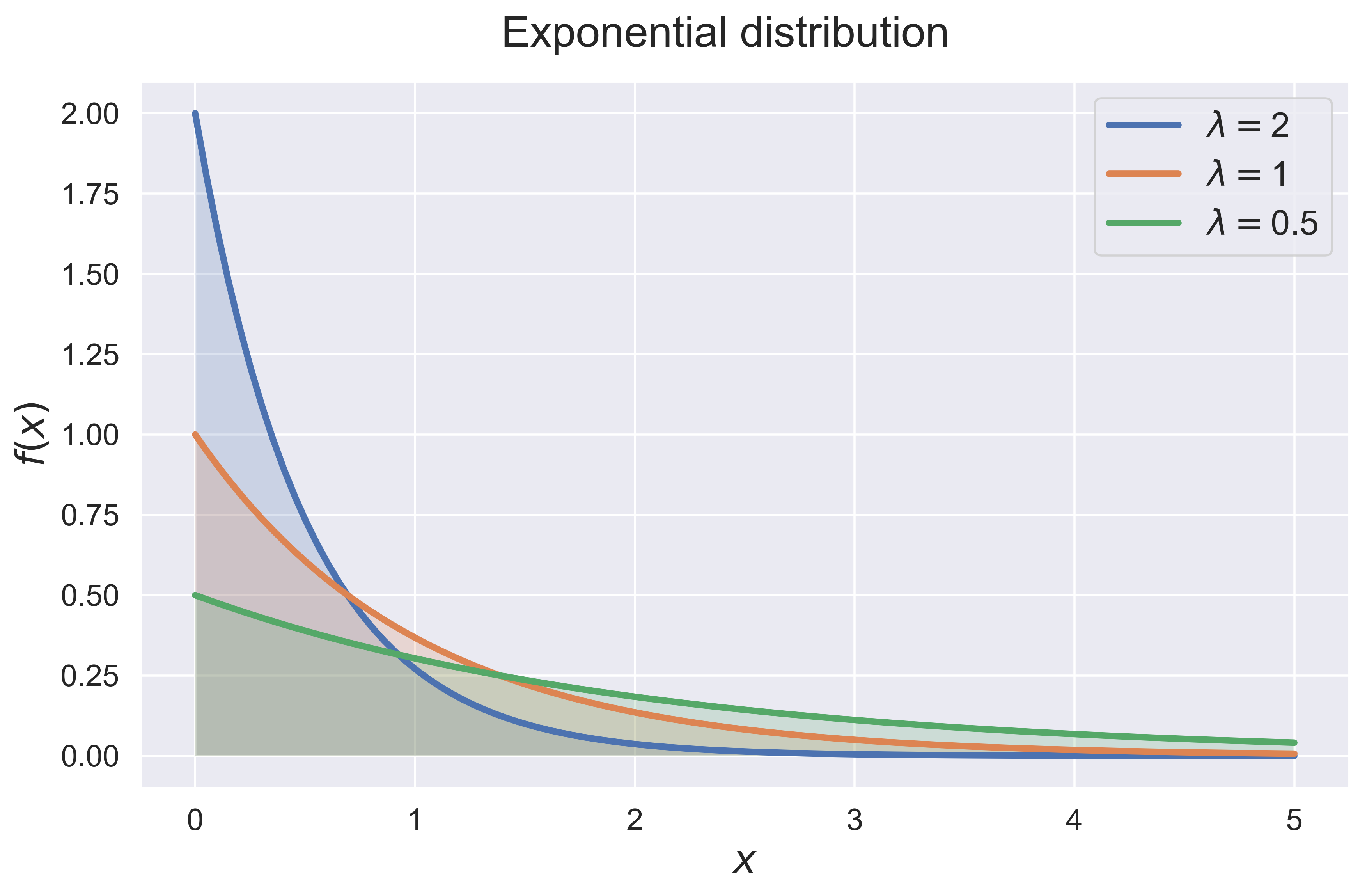
Exponential Distribution
figure_exponential(fsize = (10, 6), fs = 20)
-
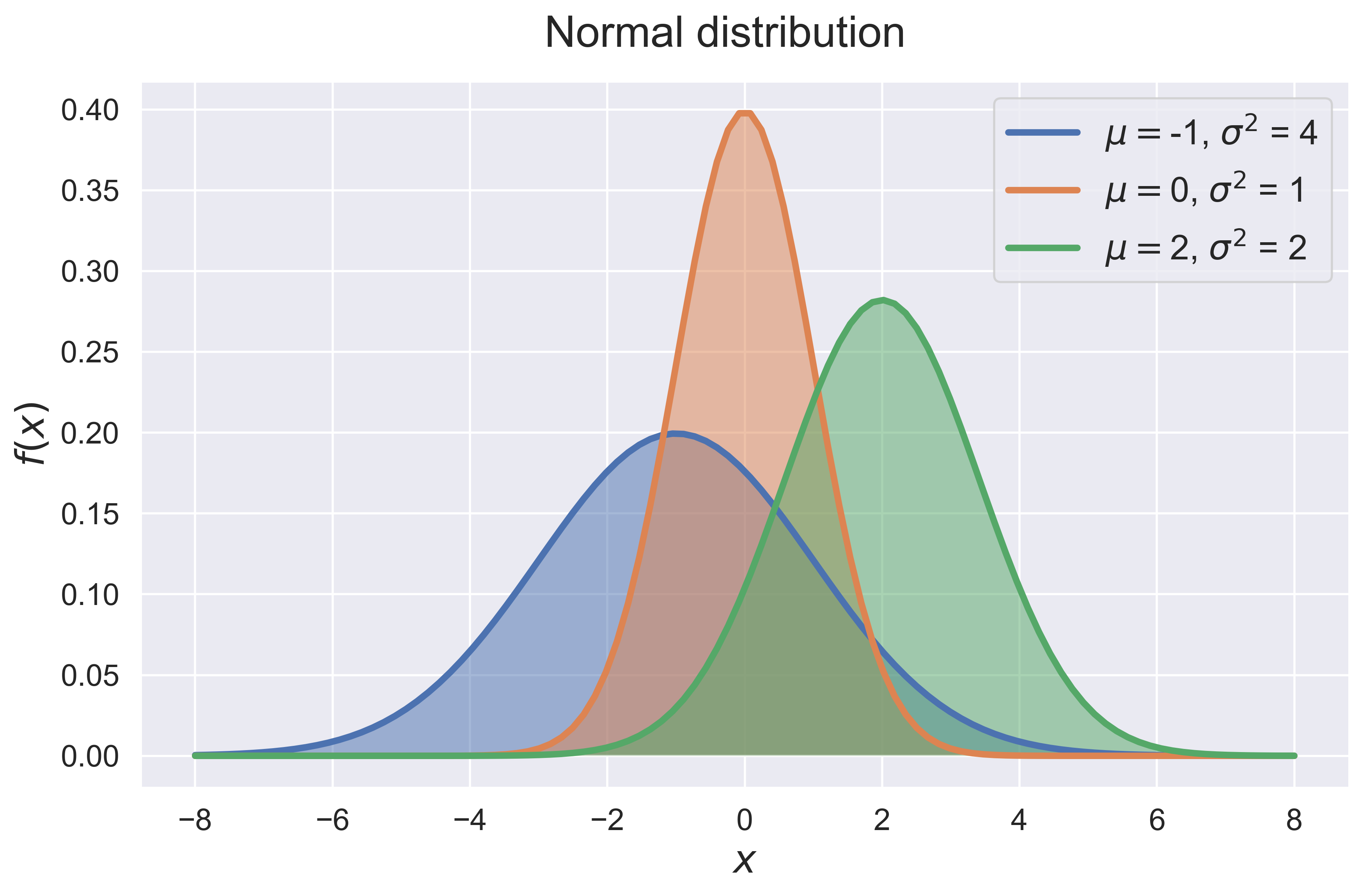
Normal Distribution
figure_normal(fsize = (10, 6), fs = 20)
-
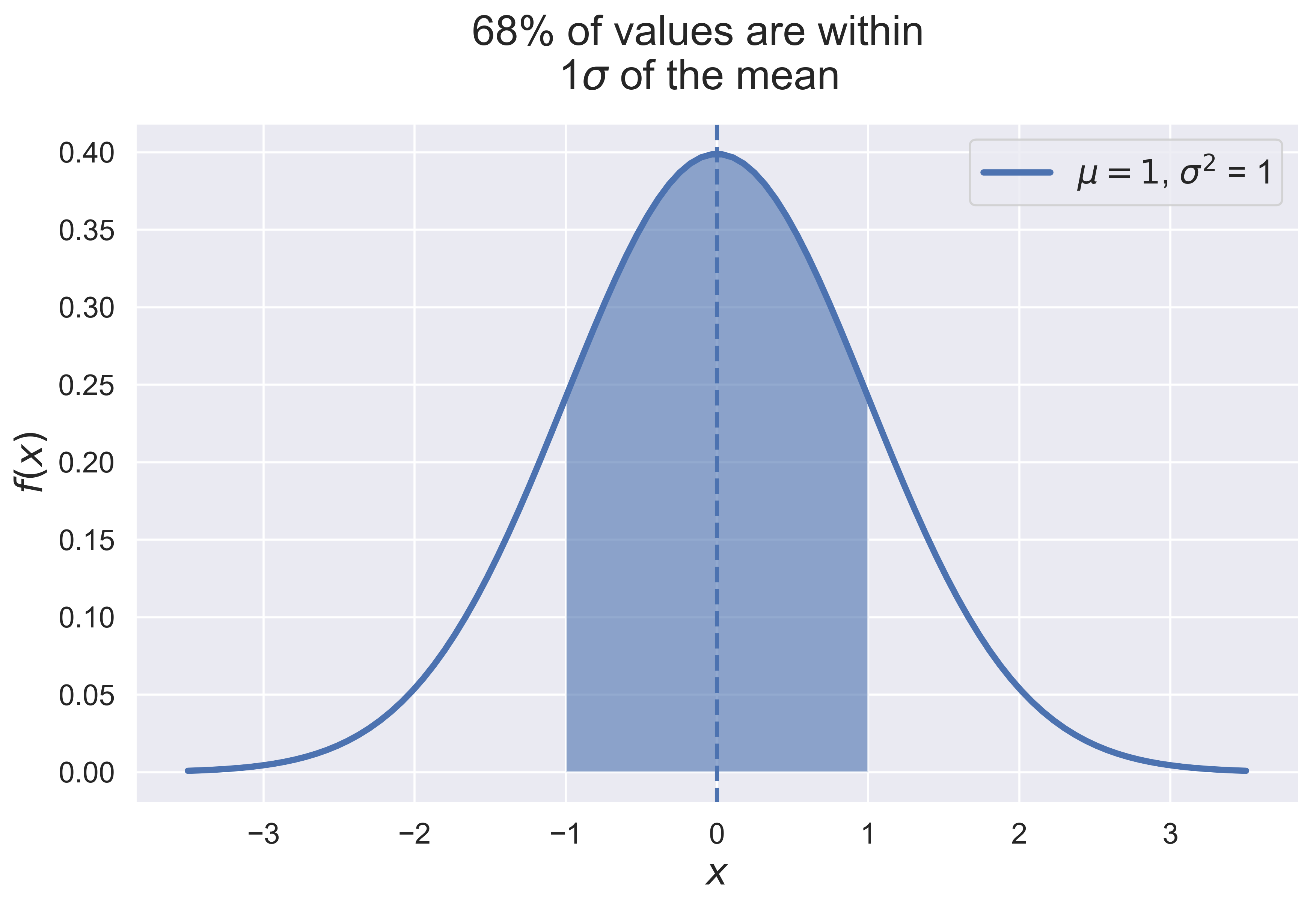
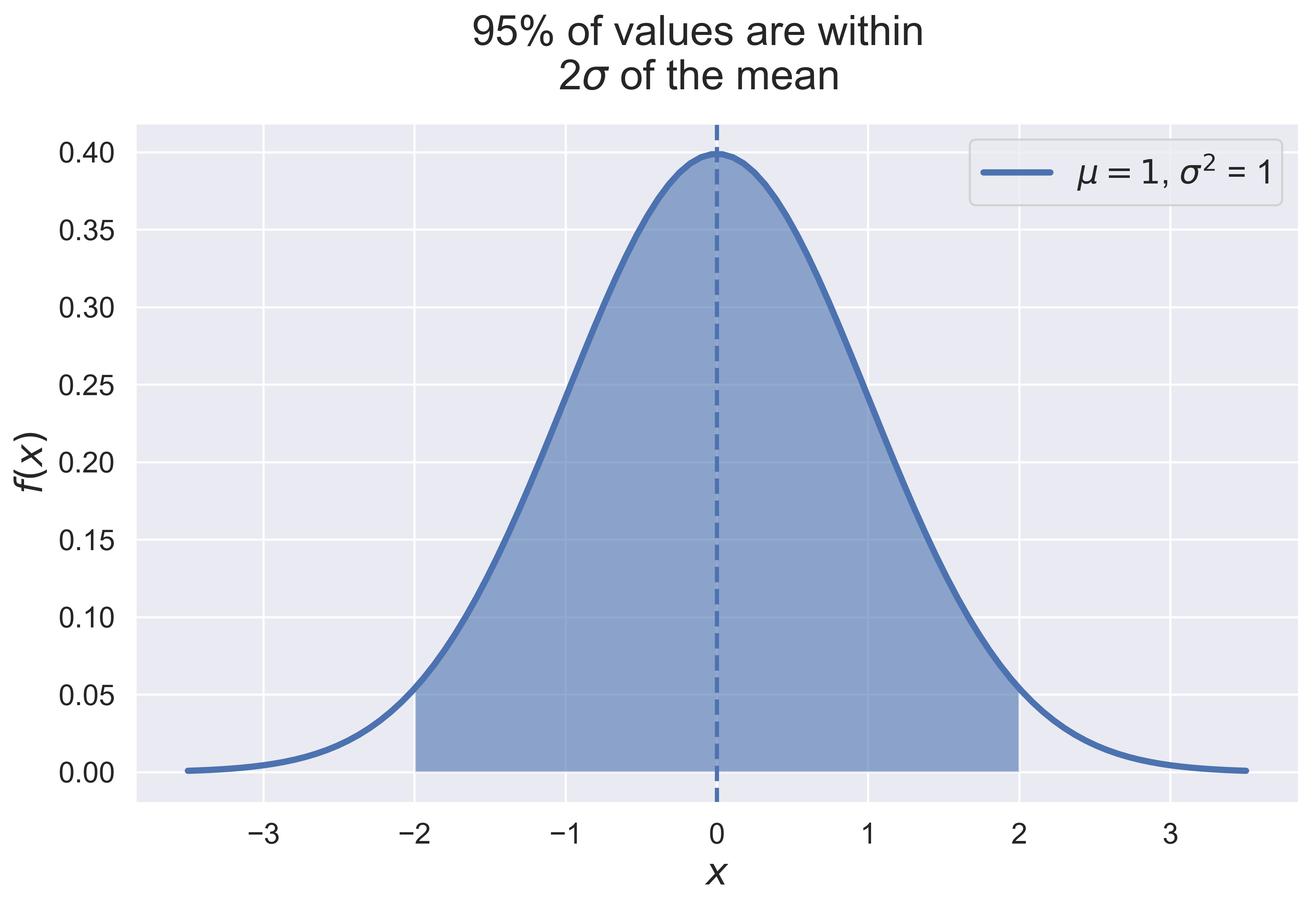
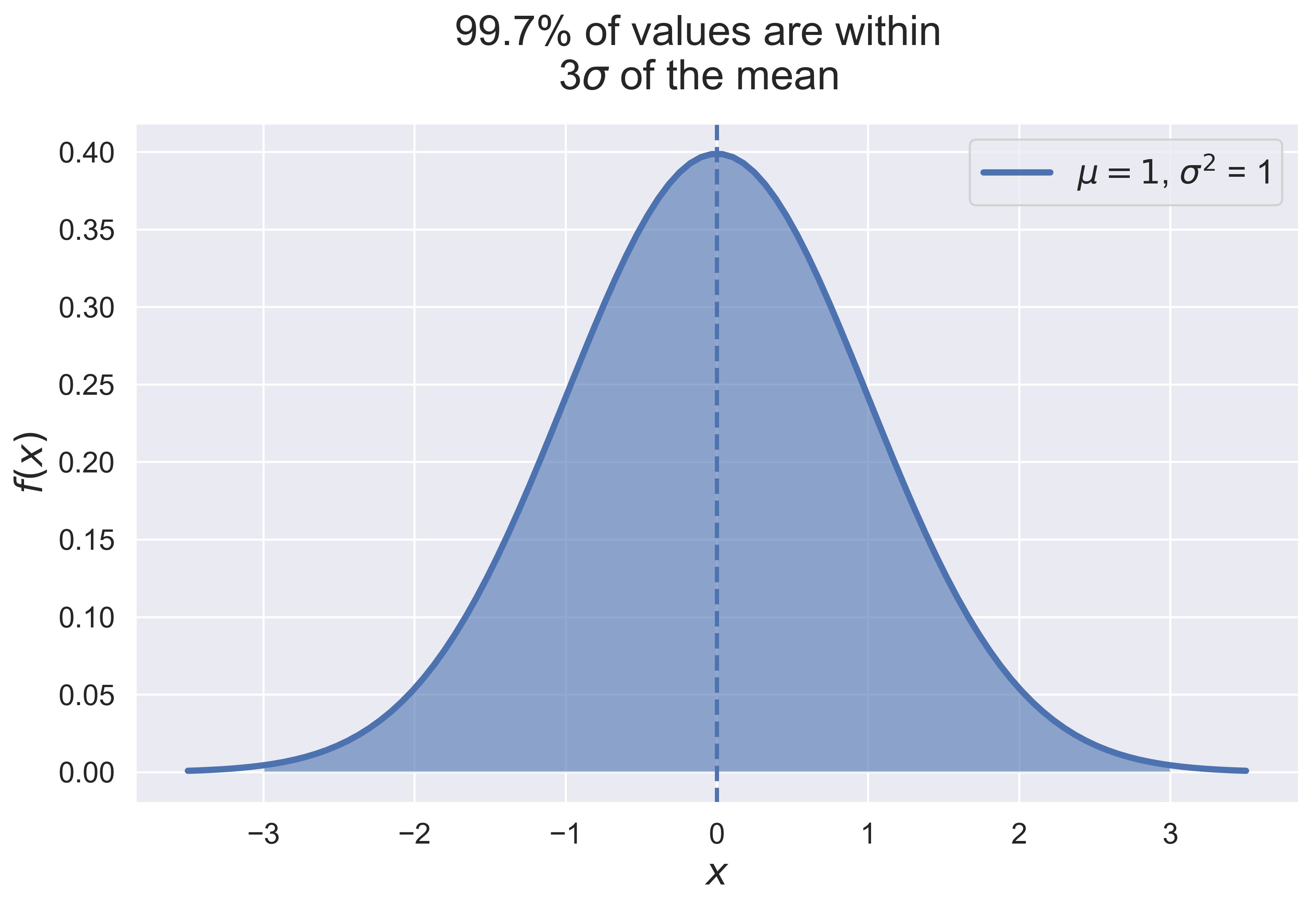
3-$\sigma$ Principle
figure_normal_sd(mu = 0, sigma = 1, c = 1, fsize = (10, 6), fs = 20)
-
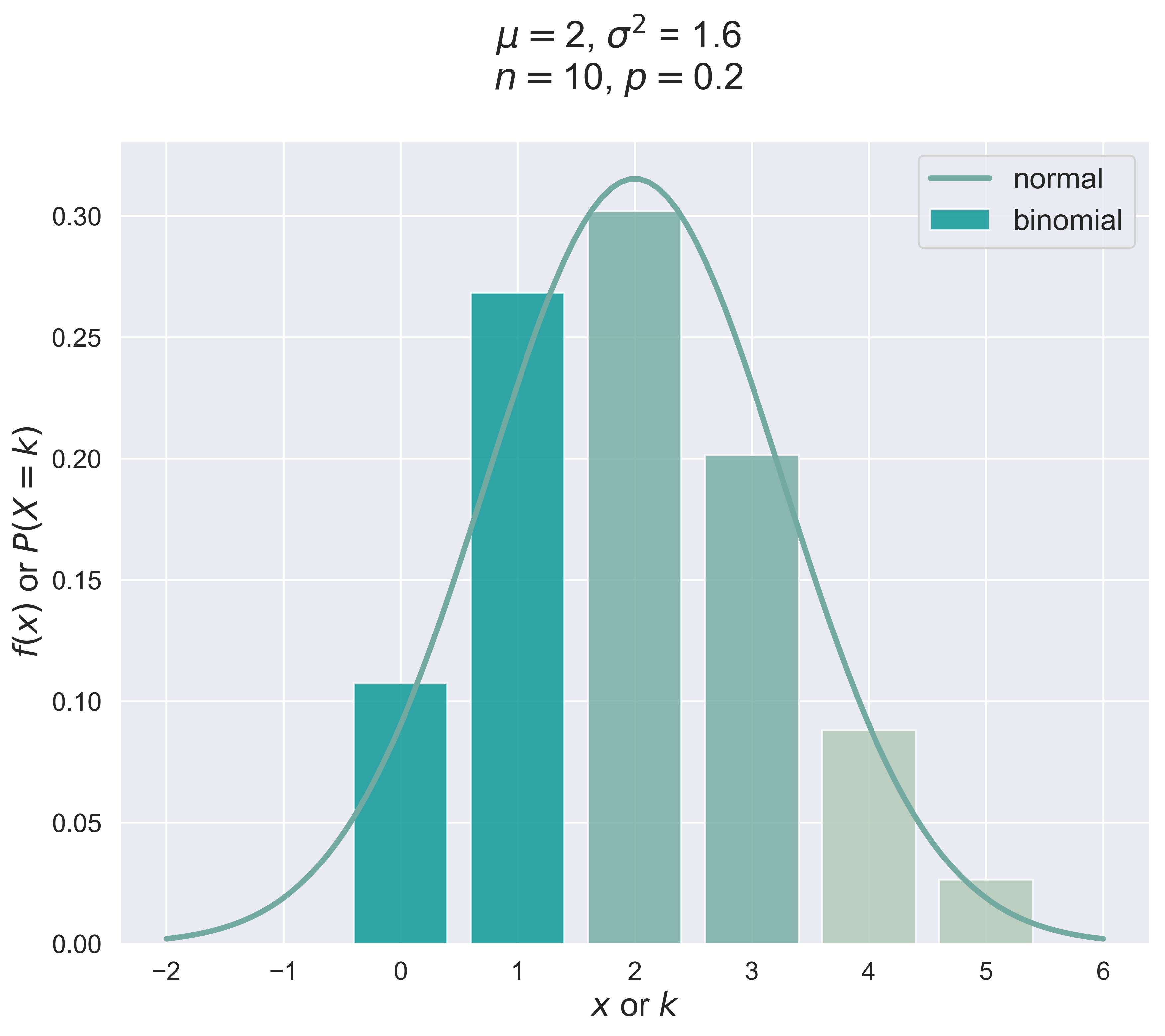
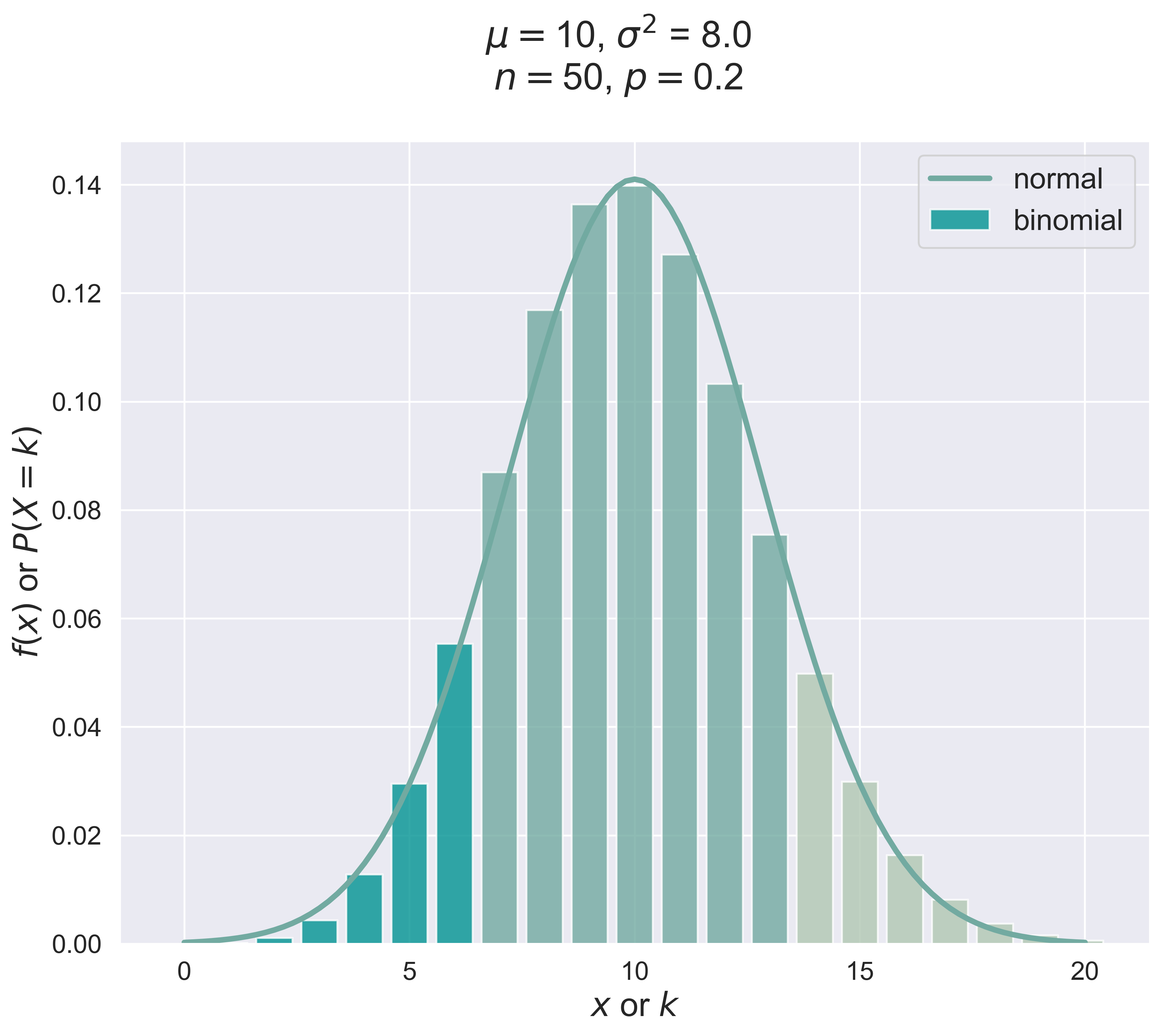
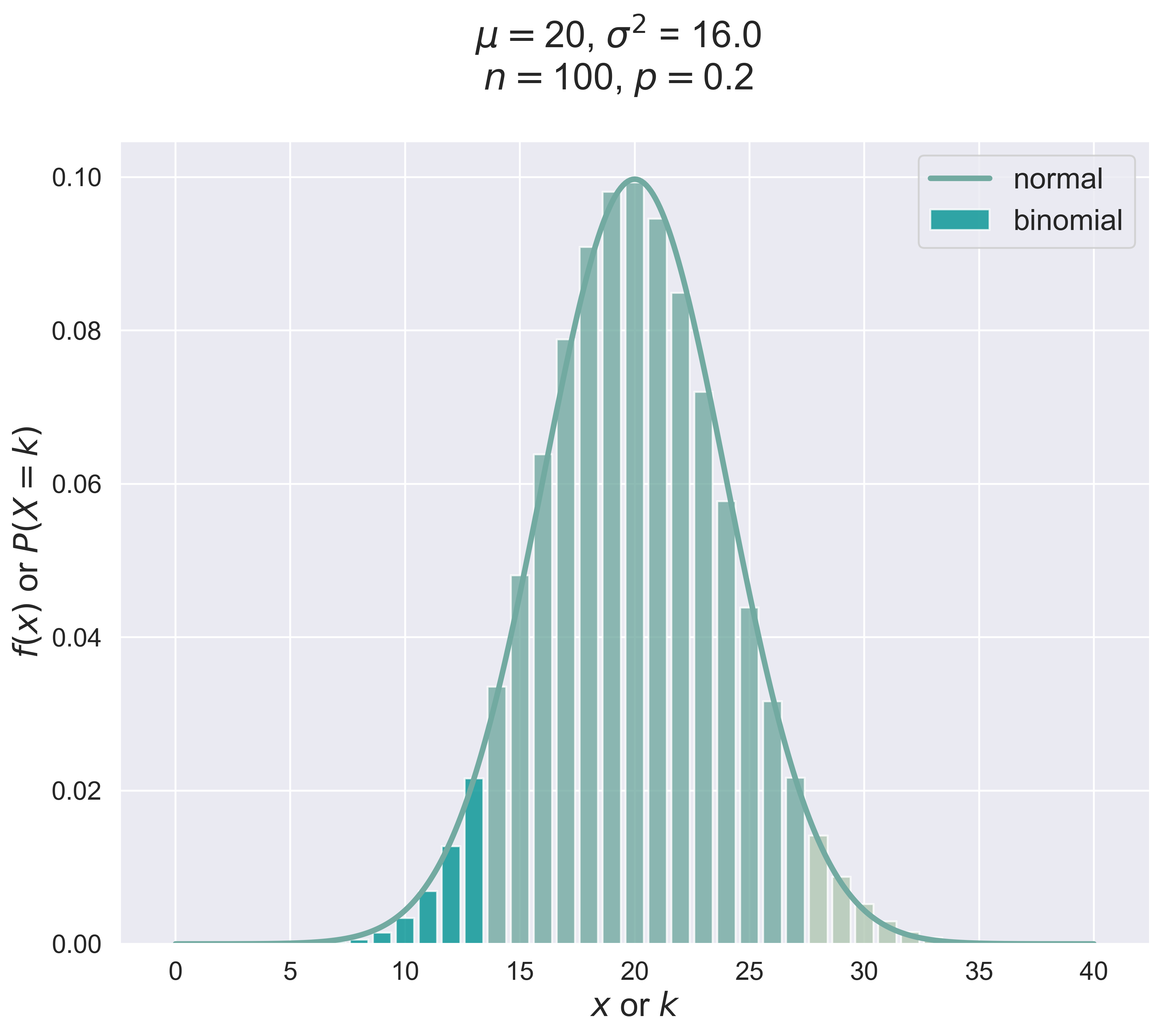
Binomial Distribution Versus Normal Distribution
binomial_normal_figure(n = 10, p = 0.2, fsize = (10, 8), fs = 20, tag = 1)
Slides 0803
-
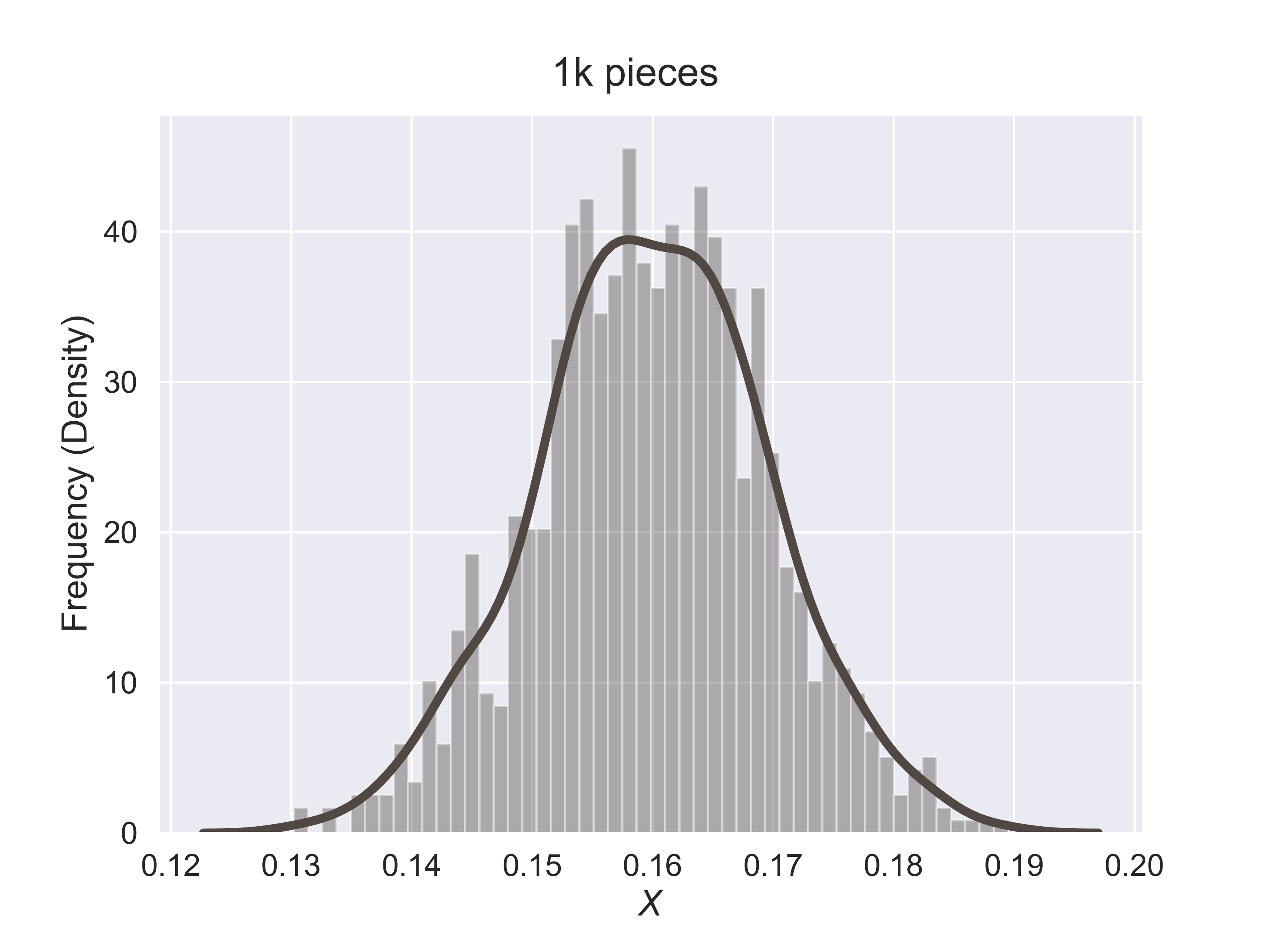
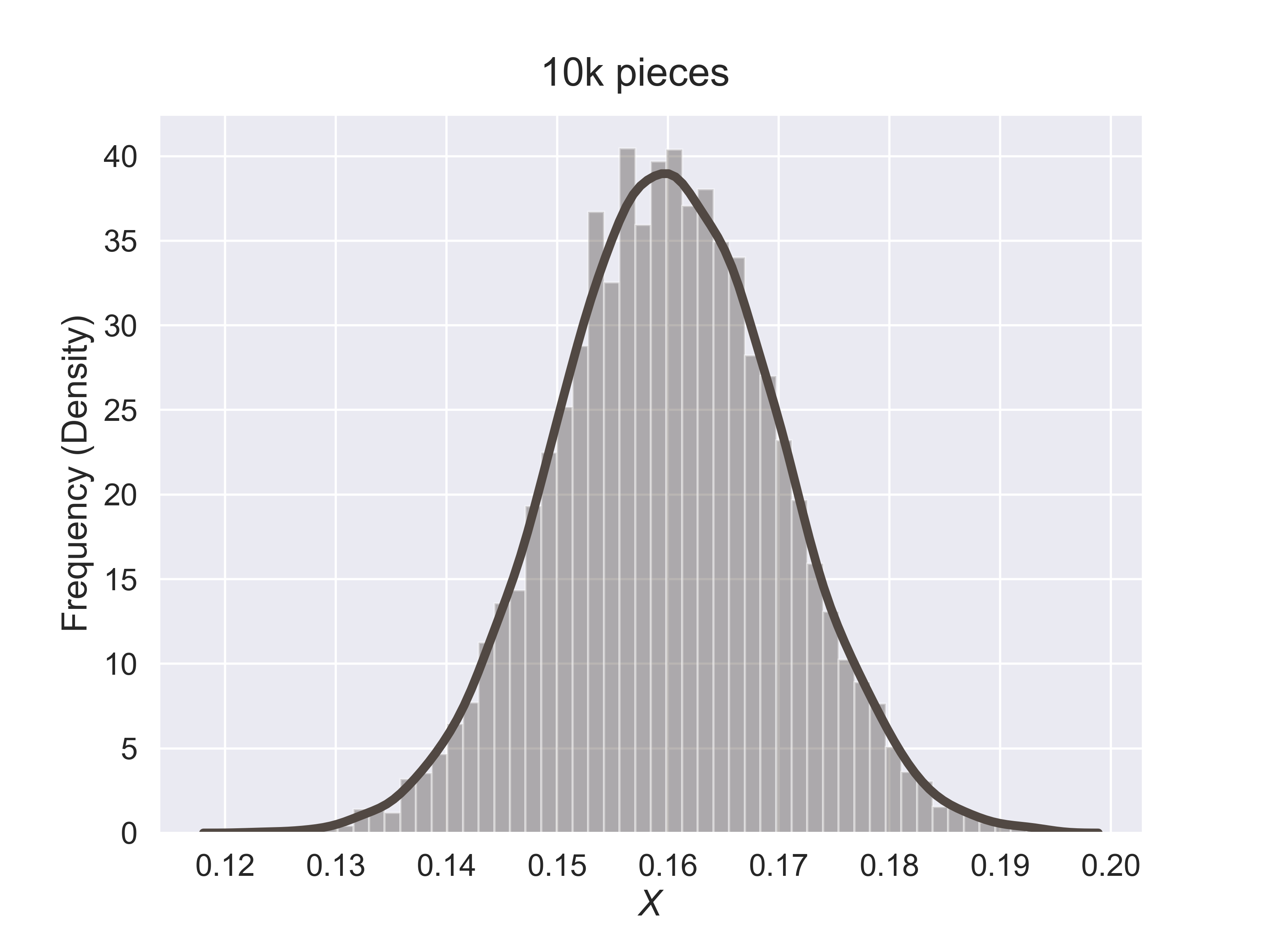
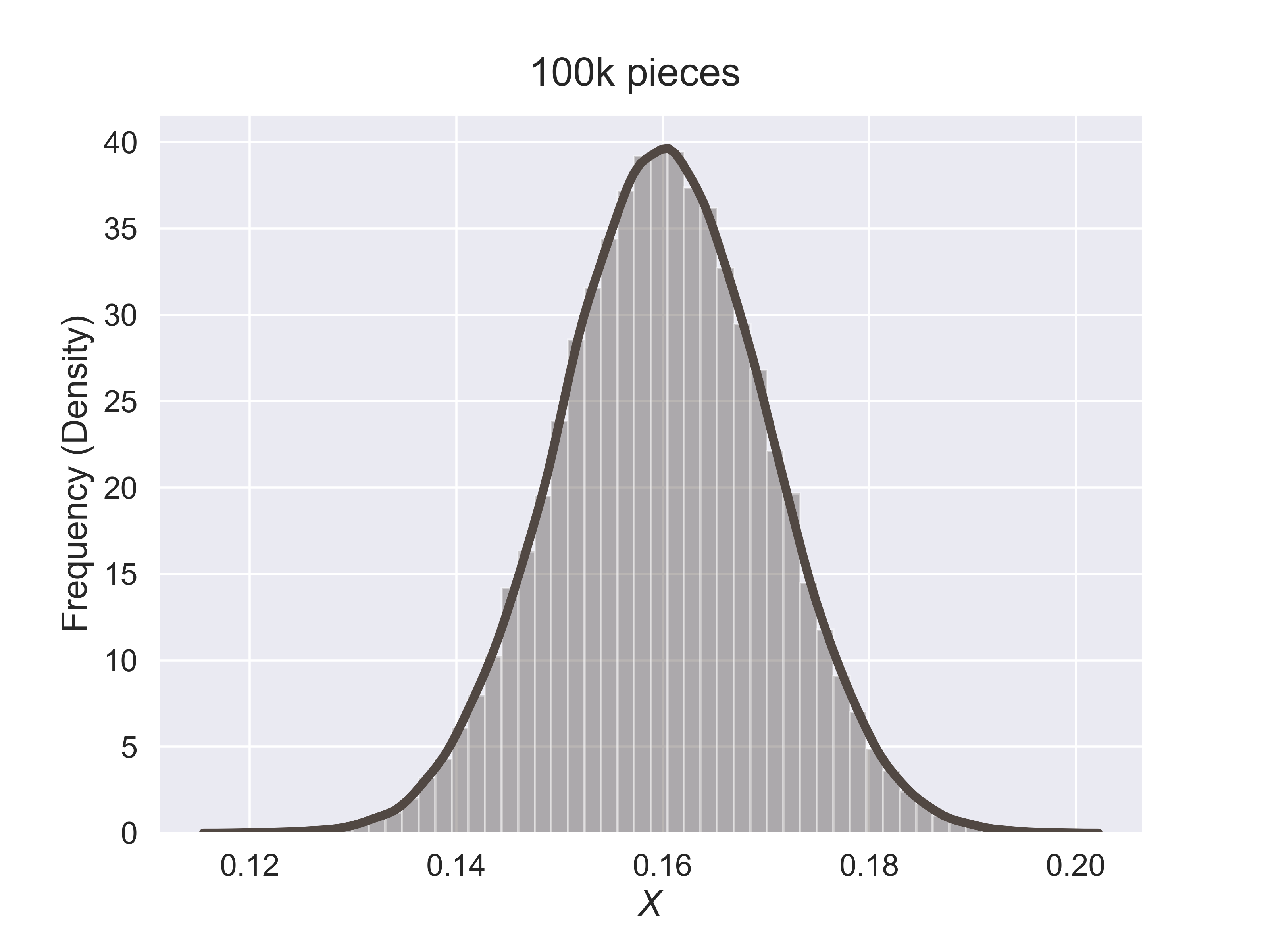
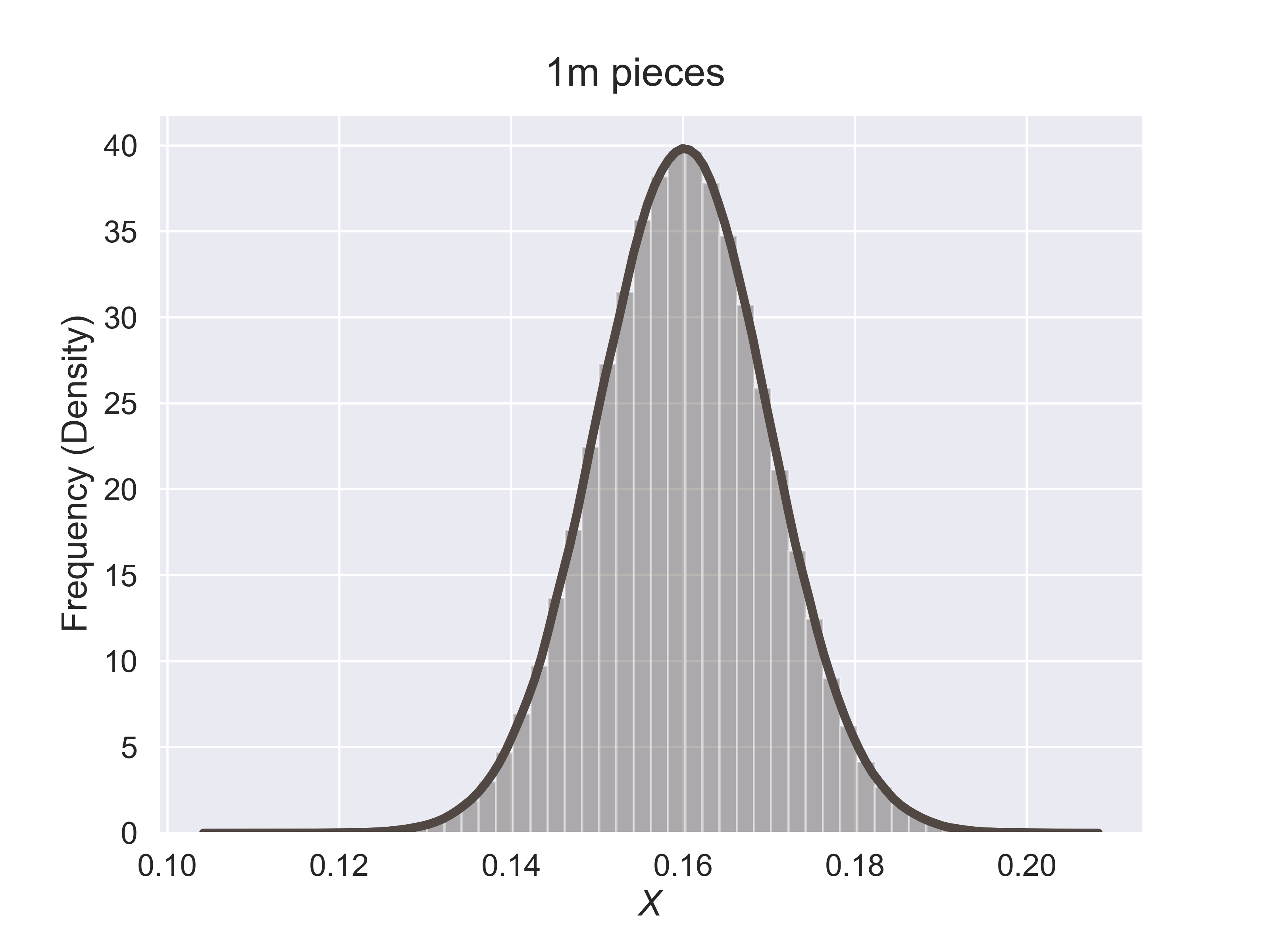
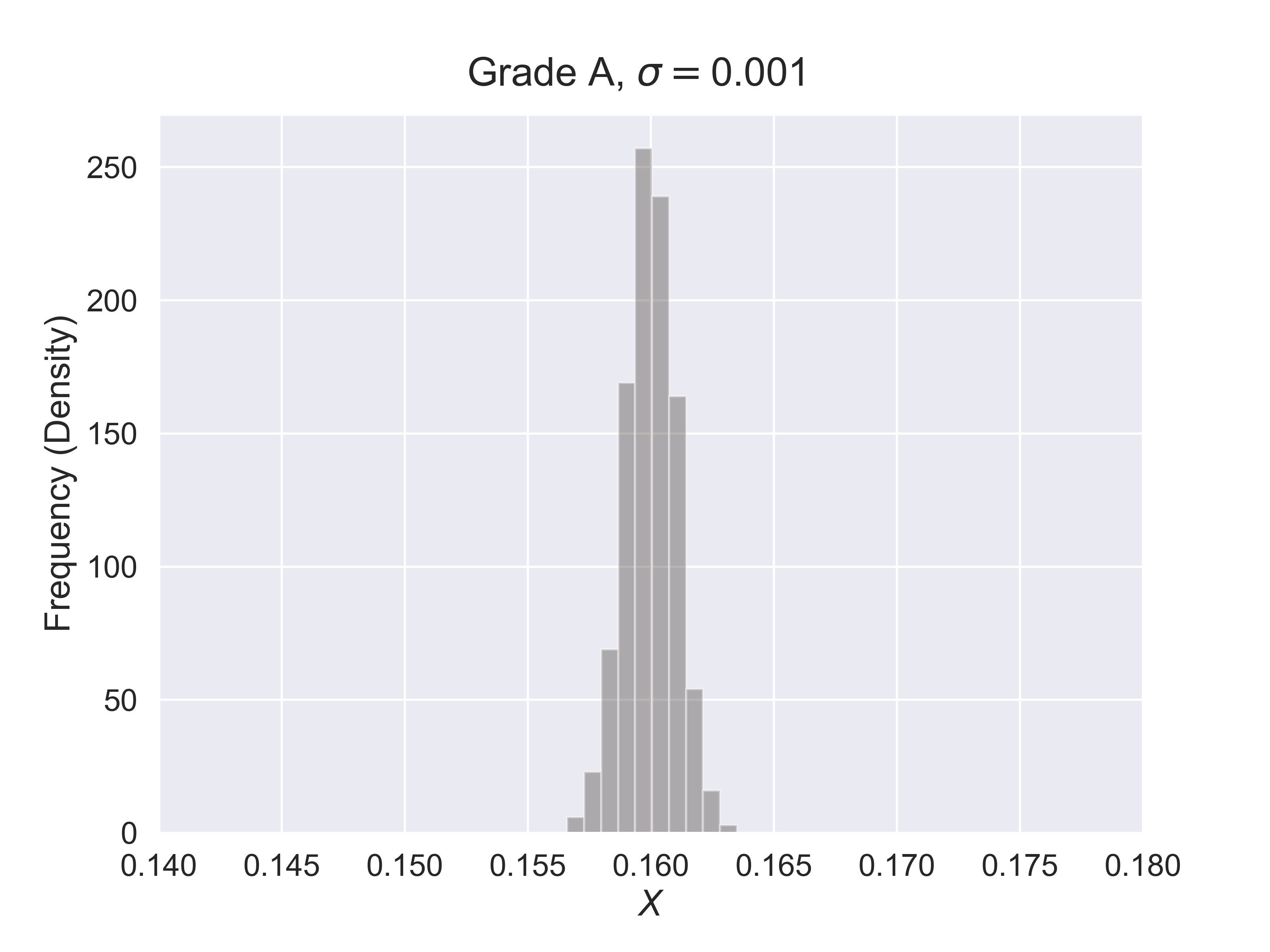
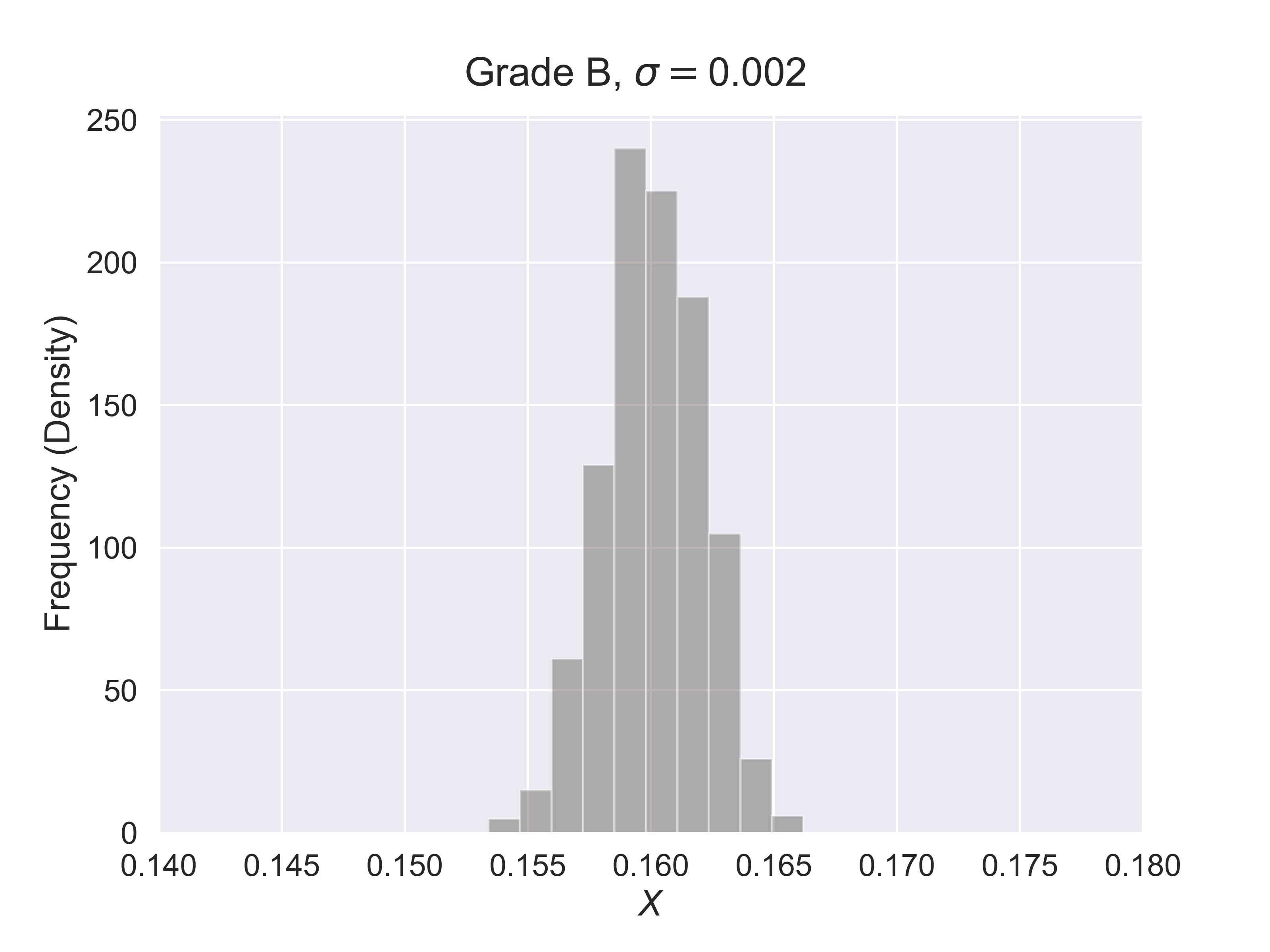
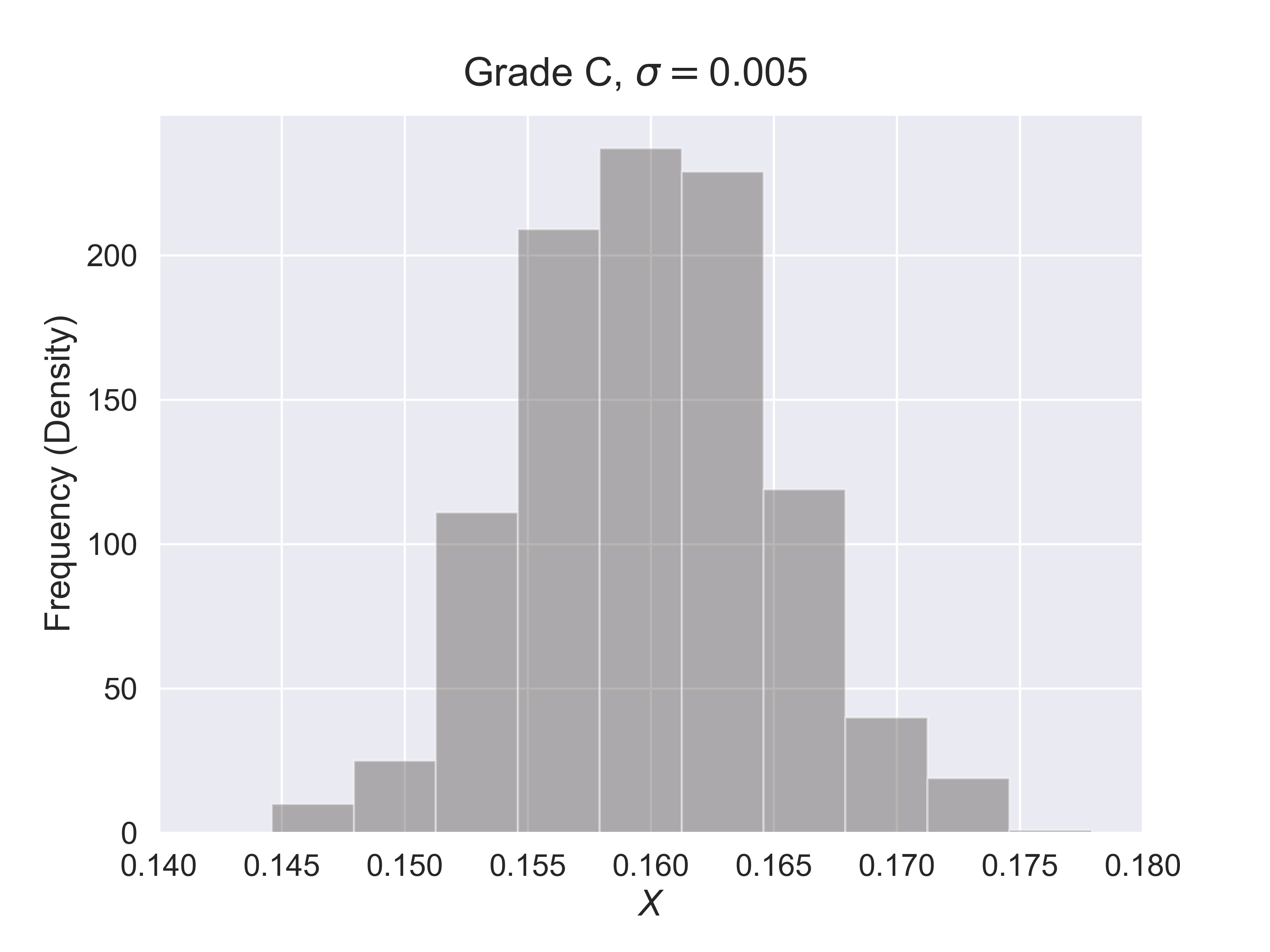
How to Estimate the Quality of Hershey Kisses?
figure_hershey_var_dist(sigma = 0.001, fsize = (8, 6), fs = 18)
Slides 0807
-
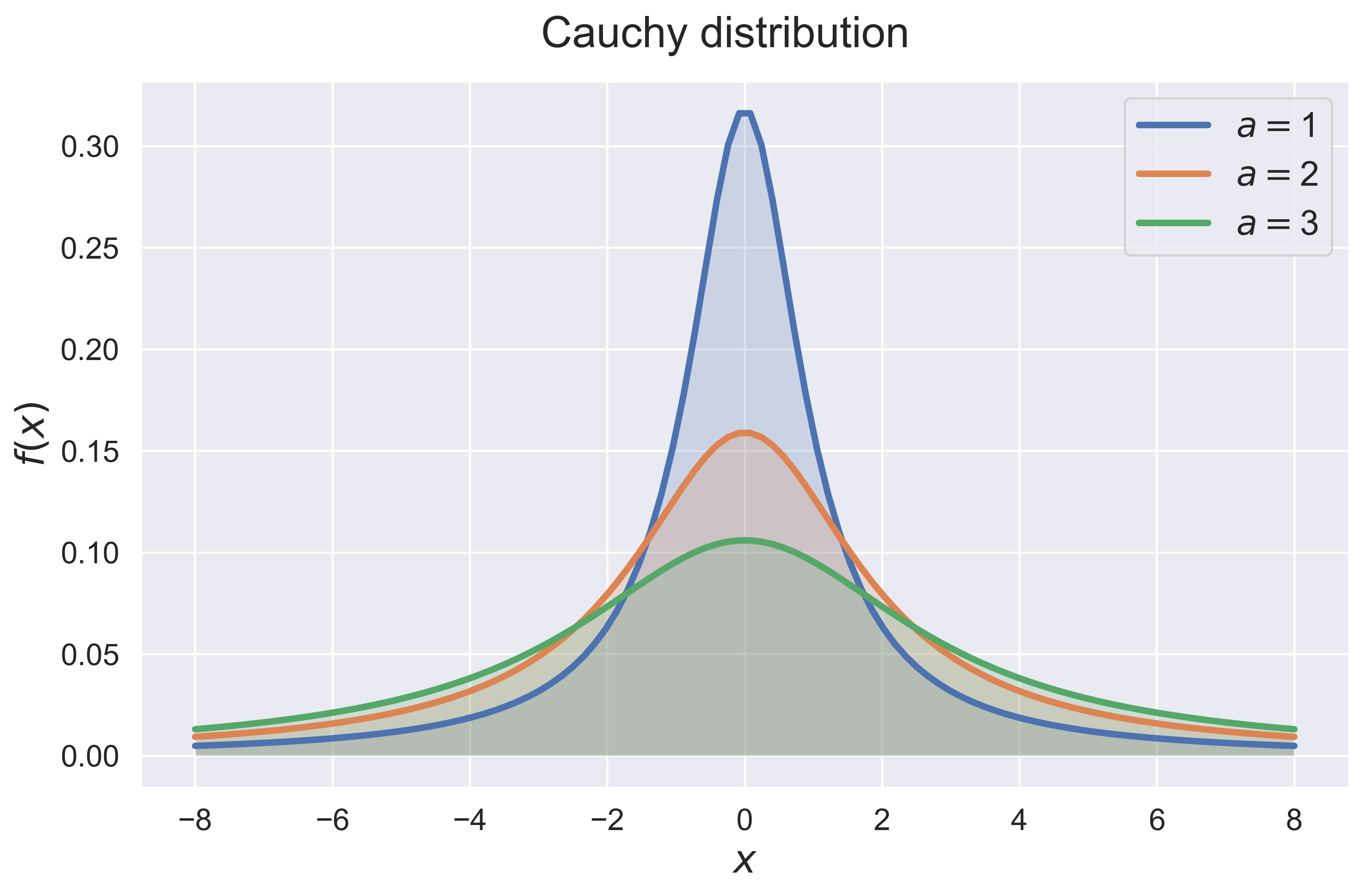
Cauchy Distribution
figure_cauchy(fsize = (10, 6), fs = 20)
-
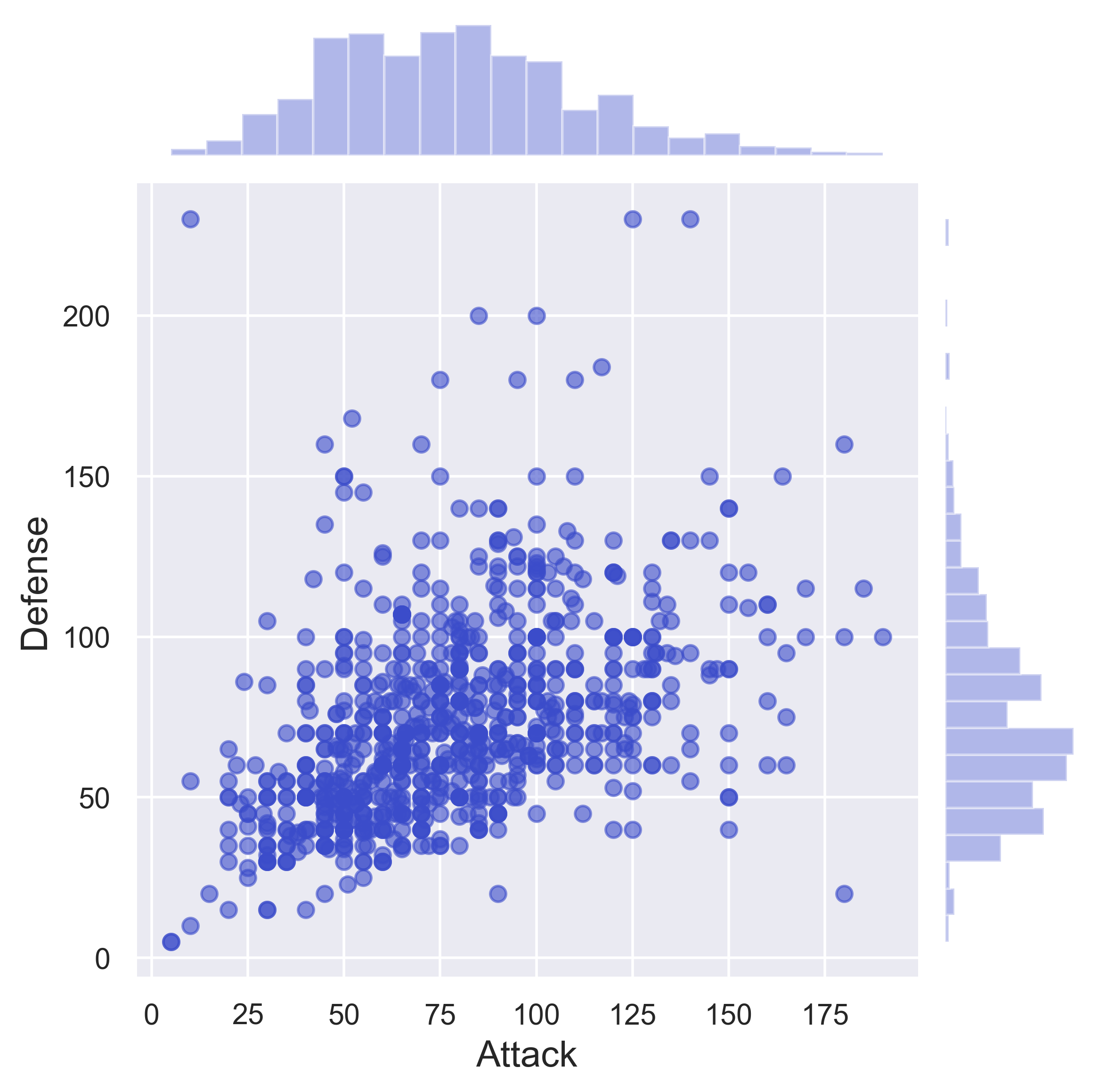
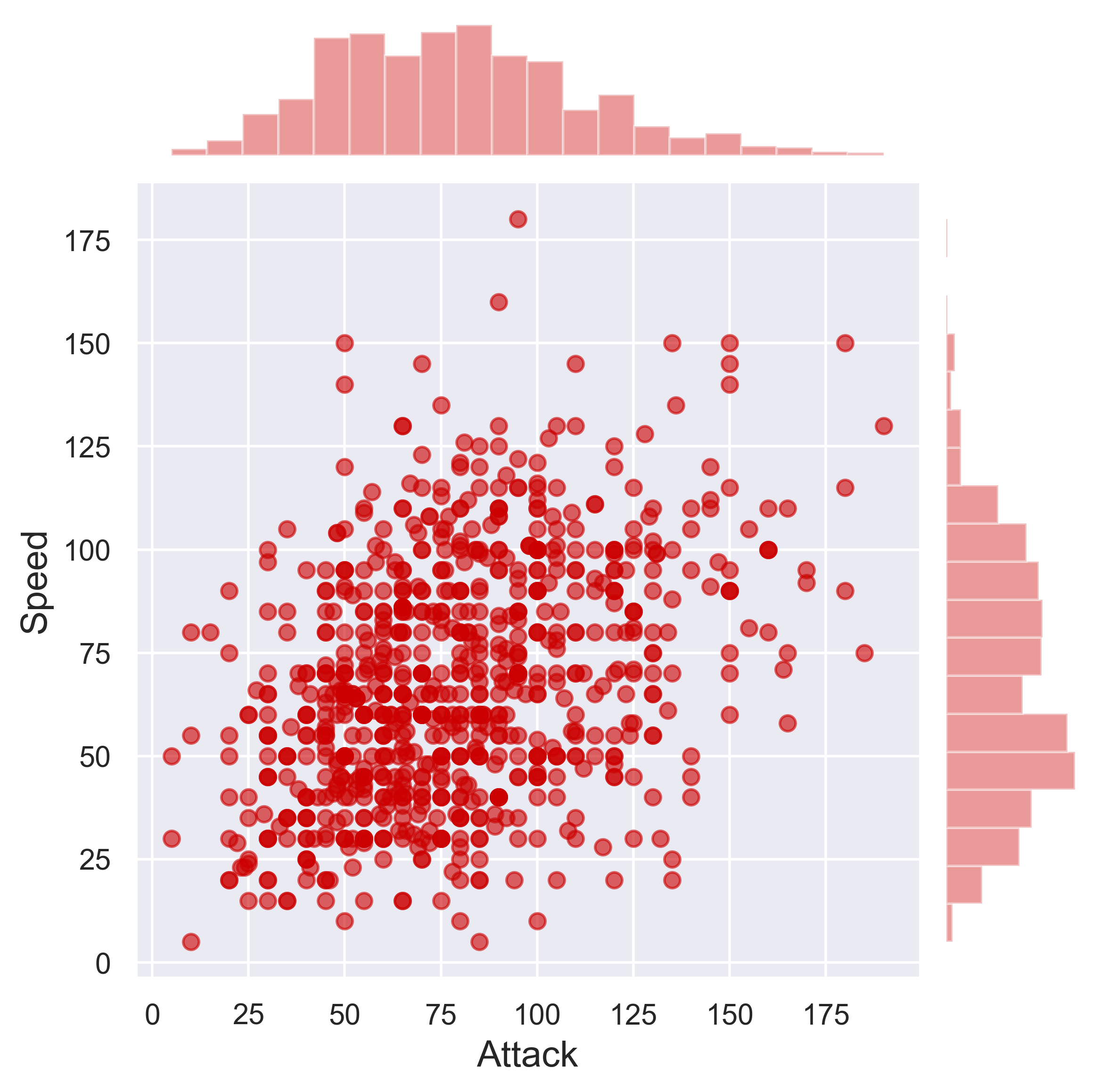
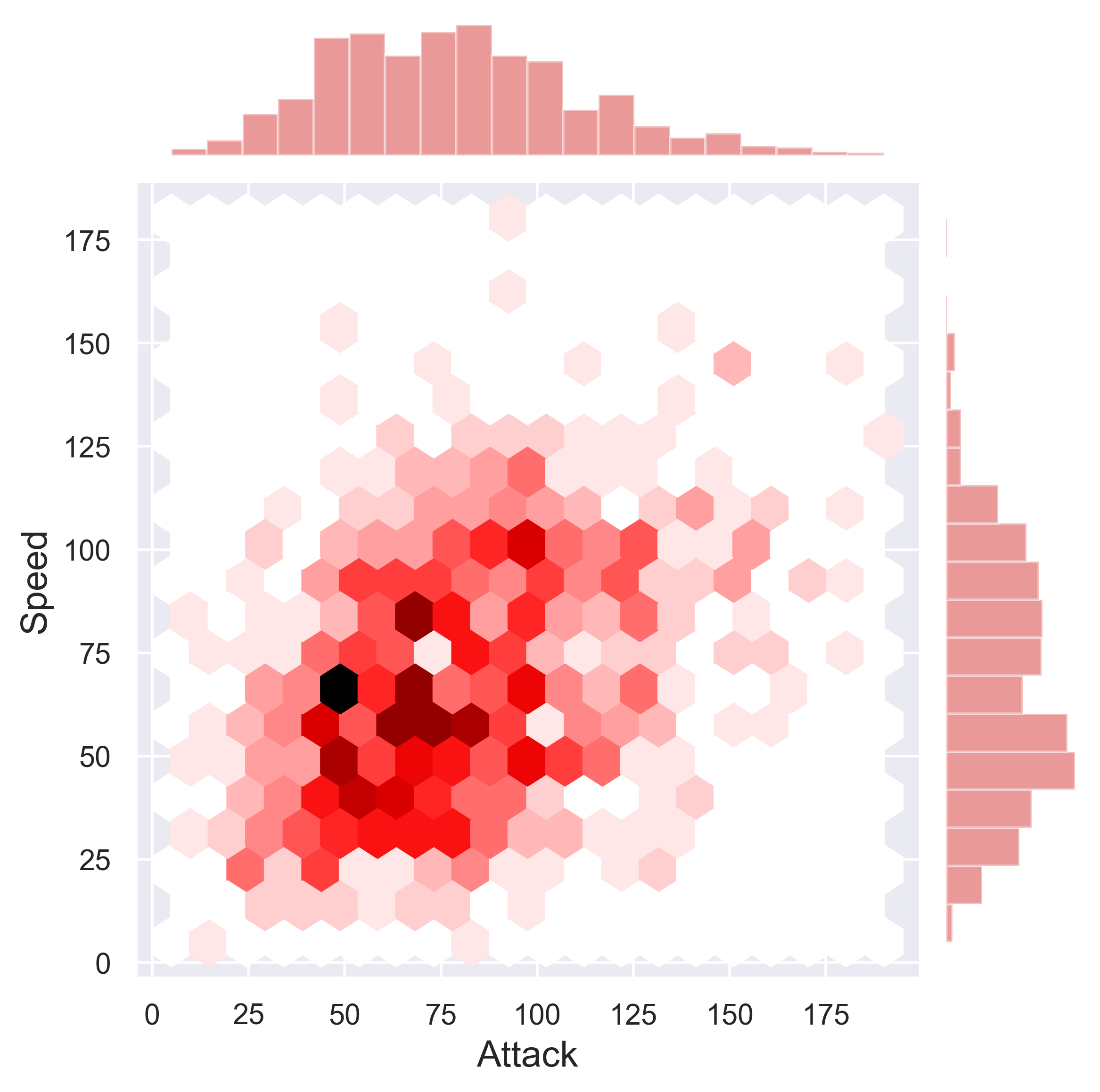
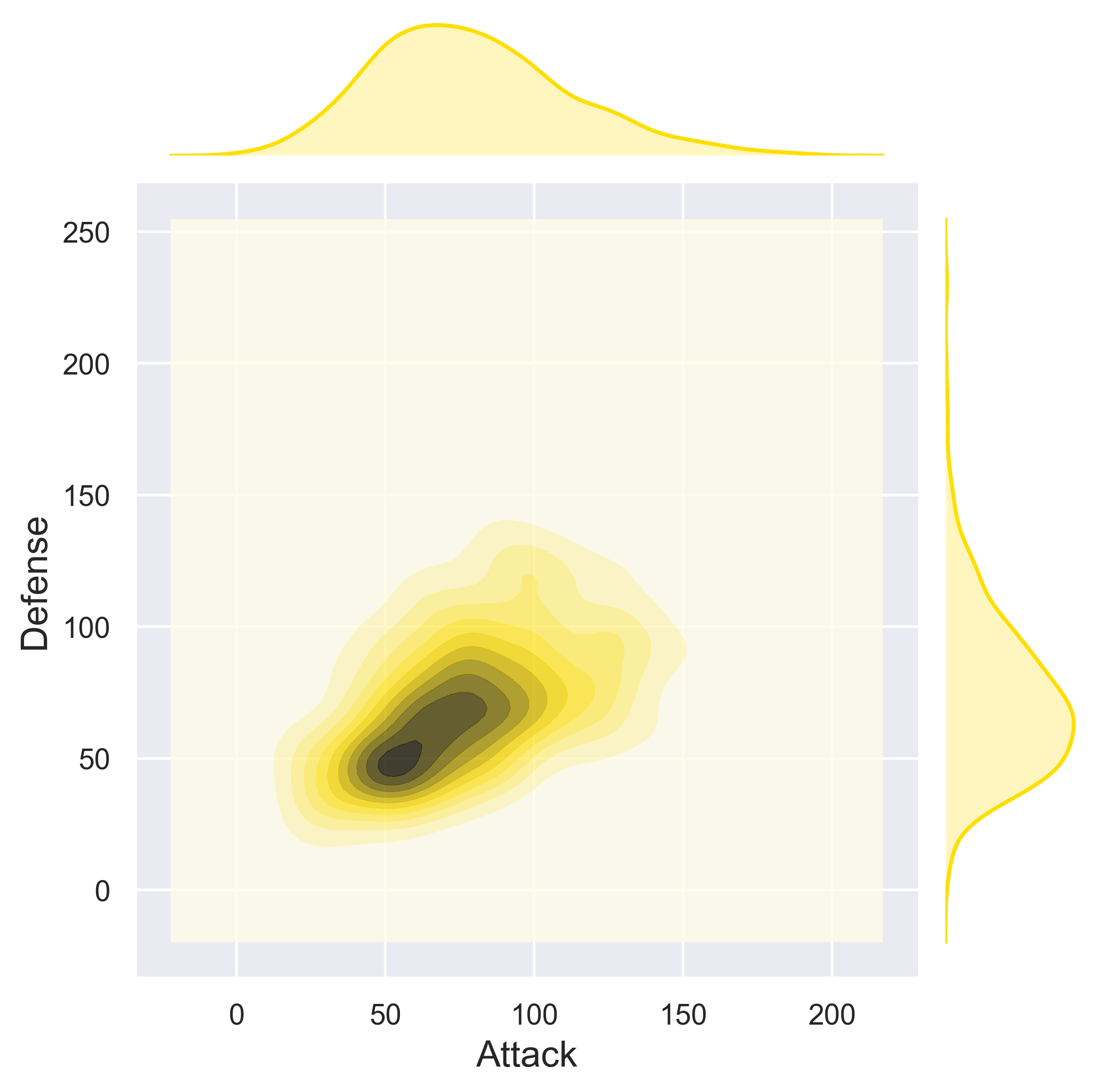
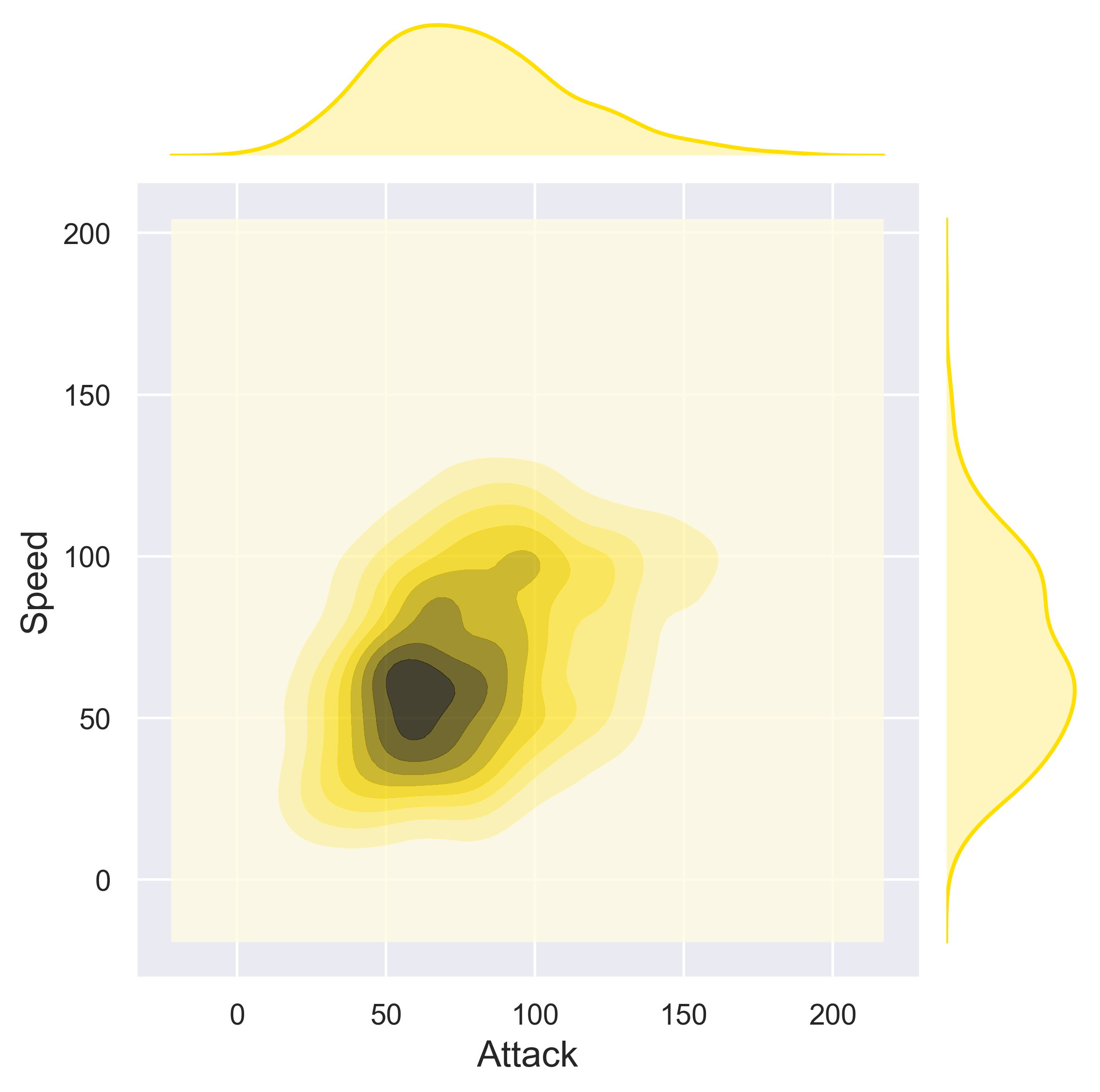
Pokemon
figure_pokemon(df = data_pokemon, column_A = 'Attack', column_B = 'Defense', job = 'scatter', fs = 16)
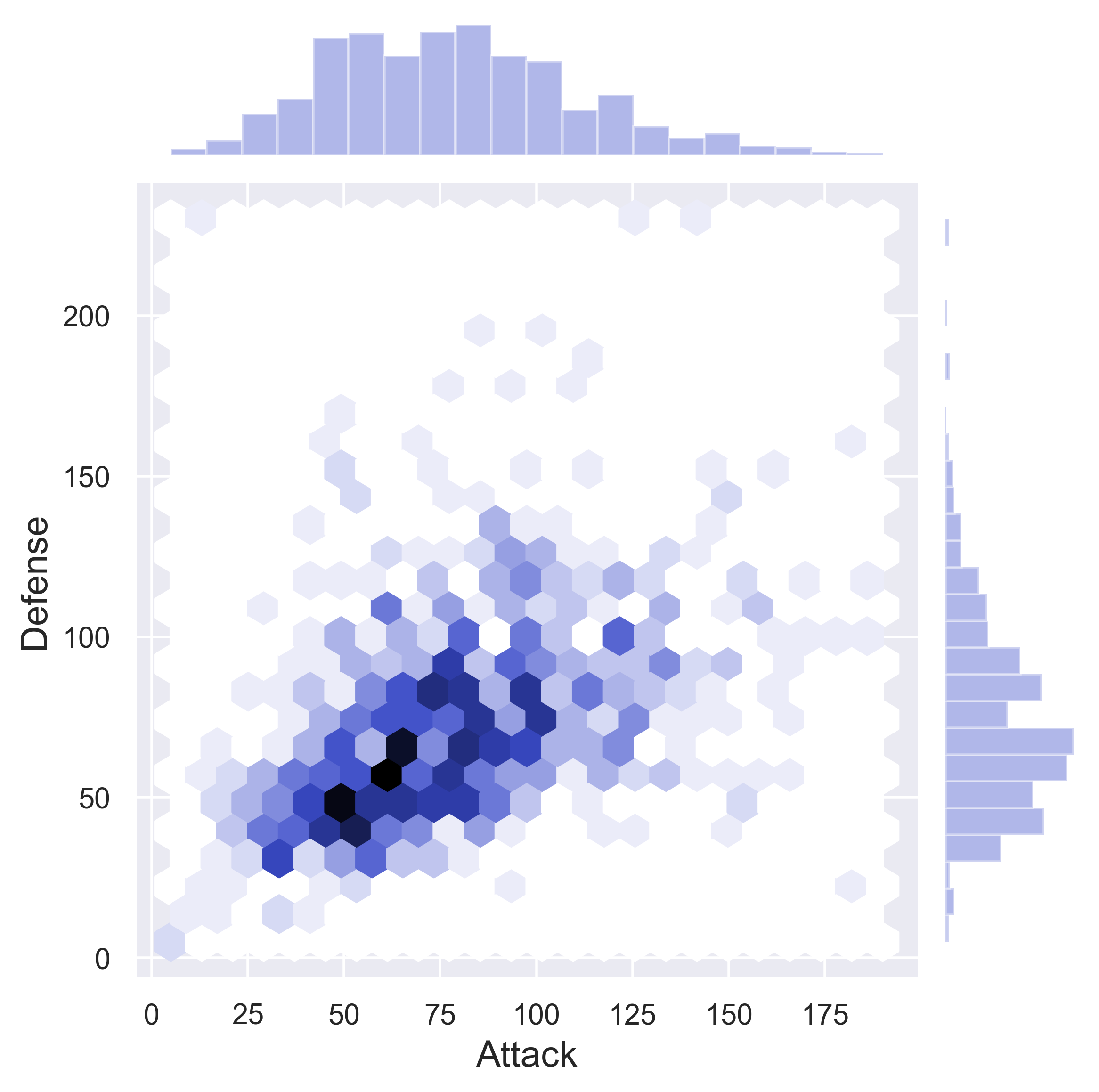
figure_pokemon(df = data_pokemon, column_A = 'Attack', column_B = 'Defense', job = 'hex', fs = 16)
figure_pokemon(df = data_pokemon, column_A = 'Attack', column_B = 'Defense', job = 'kde', fs = 16)
-
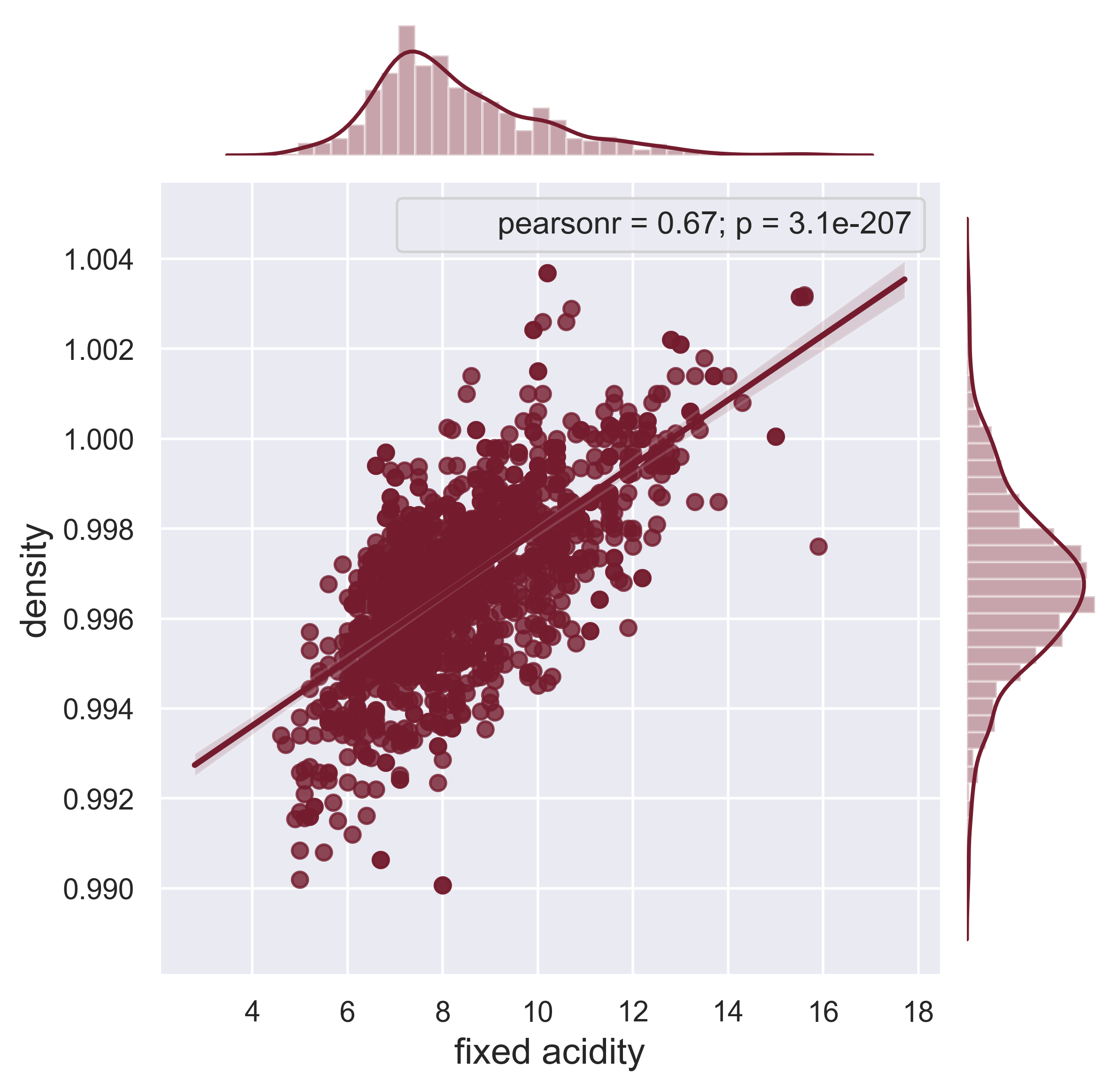
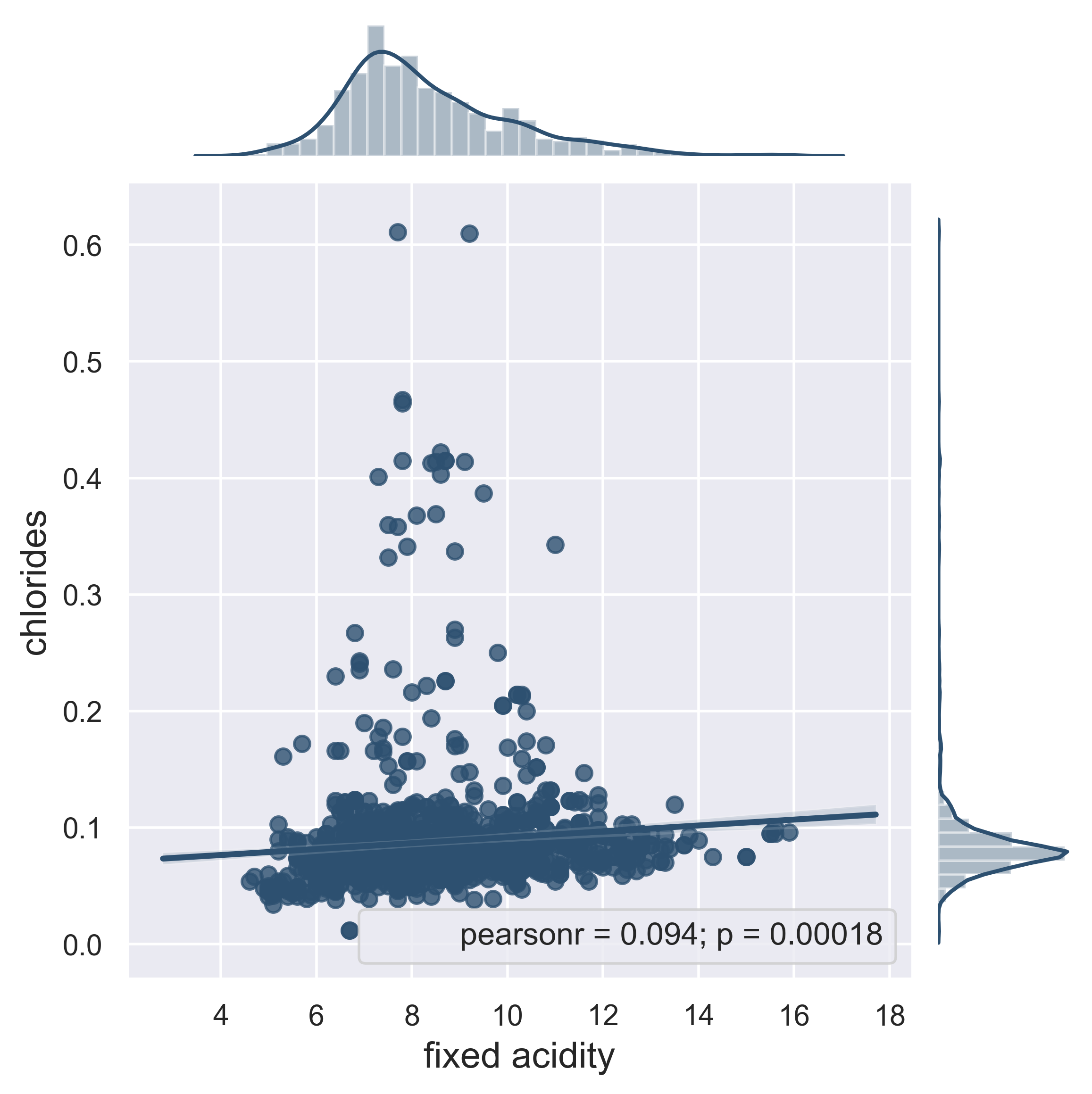
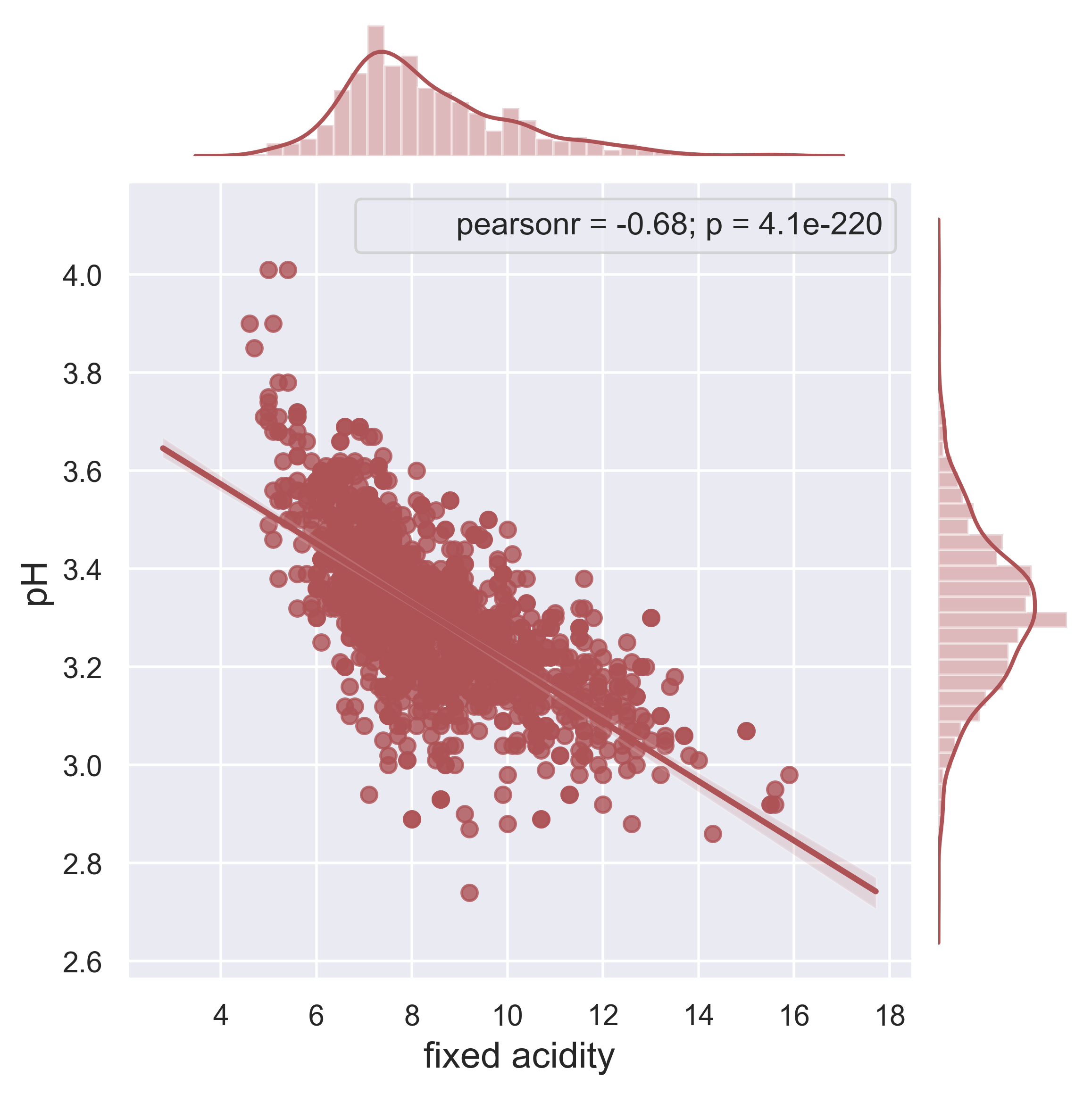
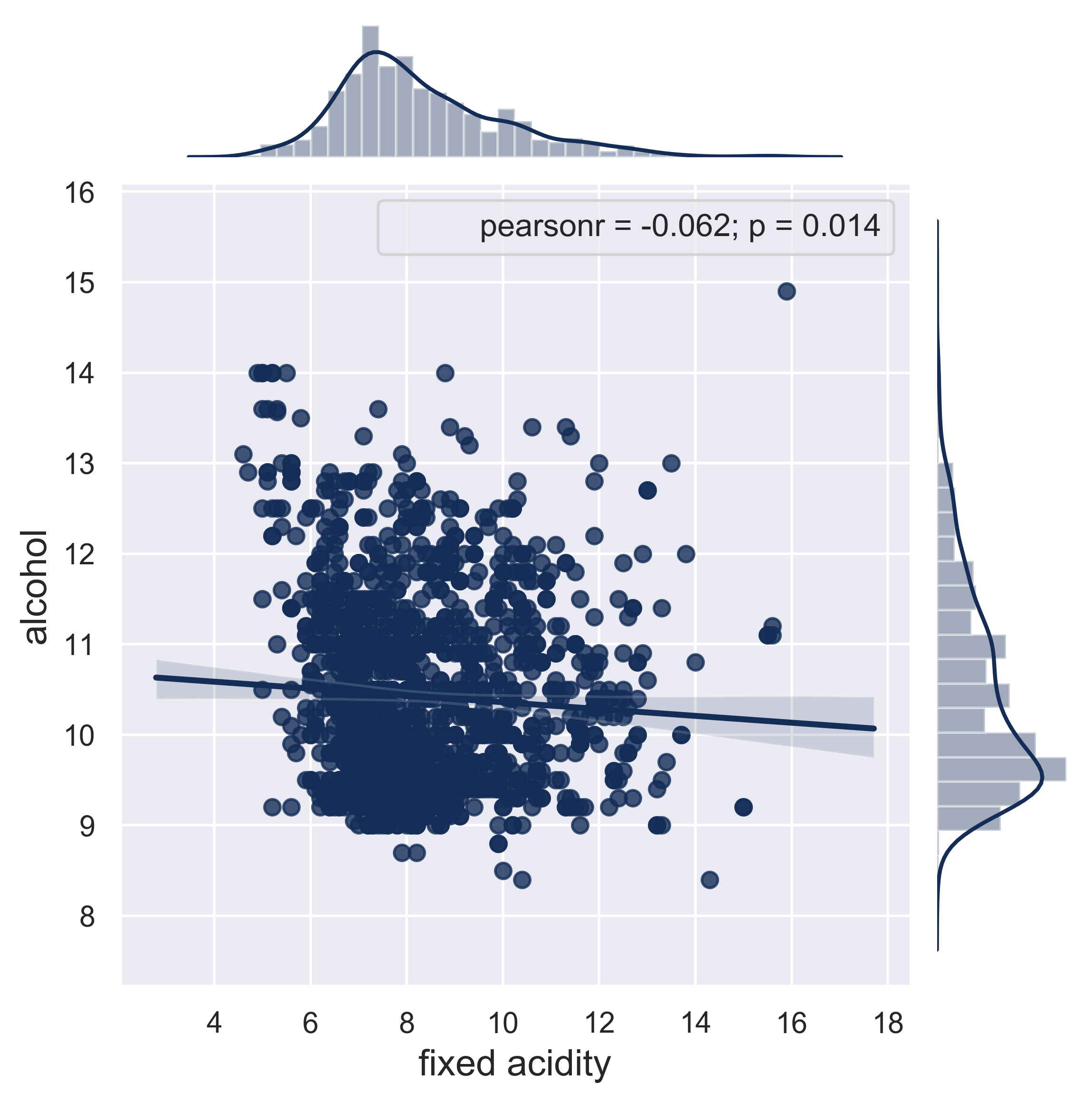
Red Wine
fig = figure_wine(df = data_wine, column_A = 'fixed acidity', column_B = 'density', job = 'reg', fs = 16)
-
Question 5 in Quiz 10
question_5_quiz_10(fsize = (10, 8), fs = 18)
Slides 0817
-
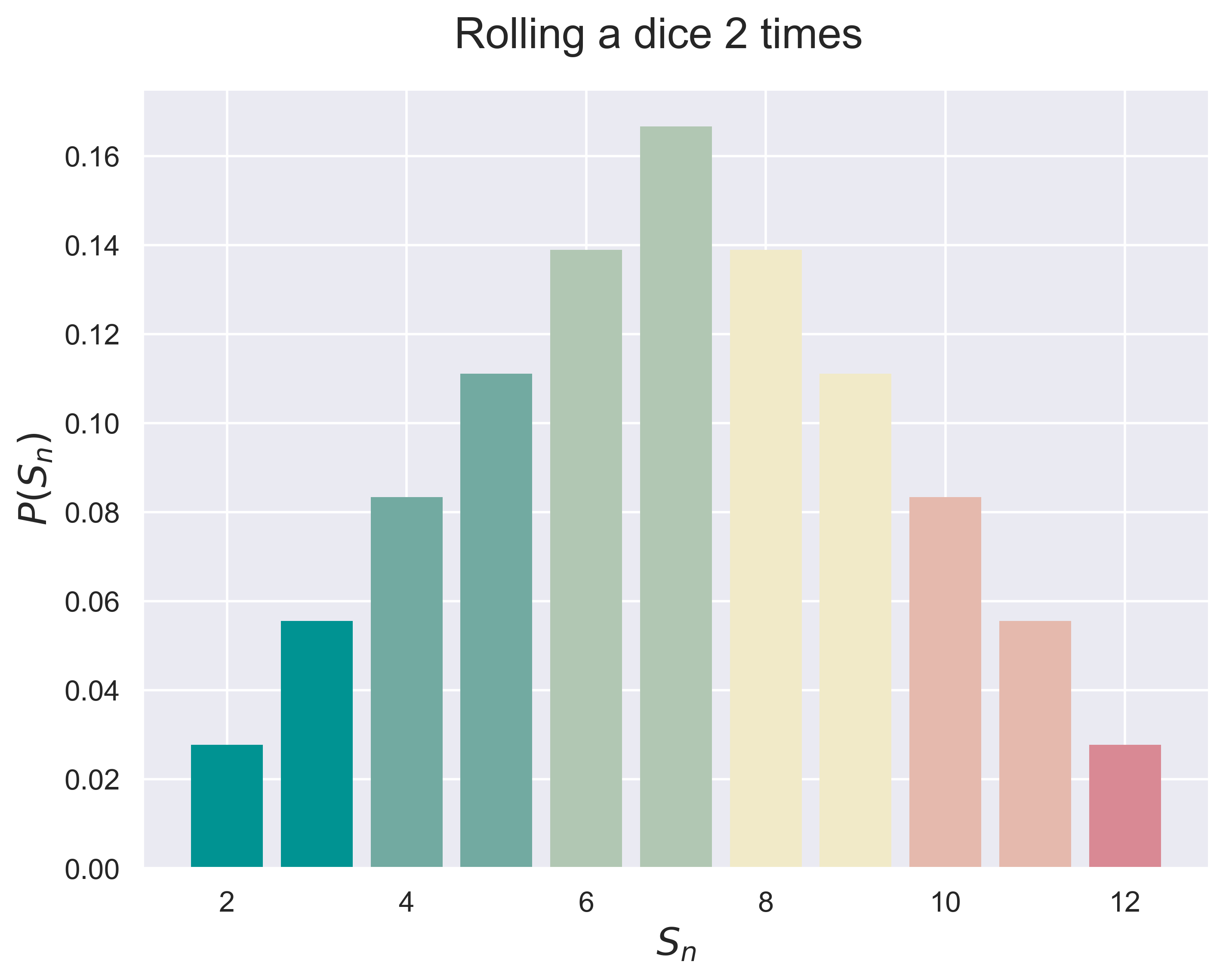
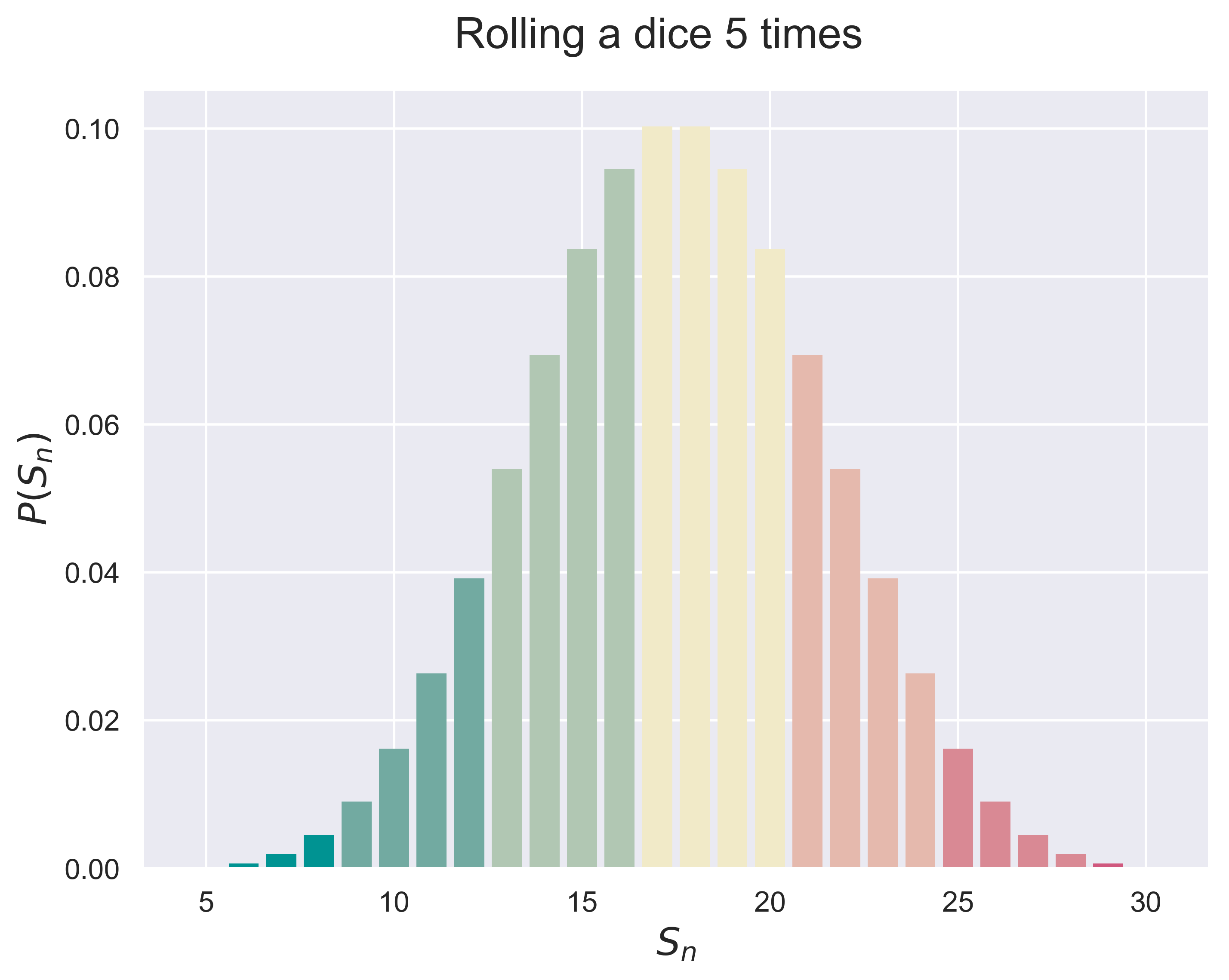
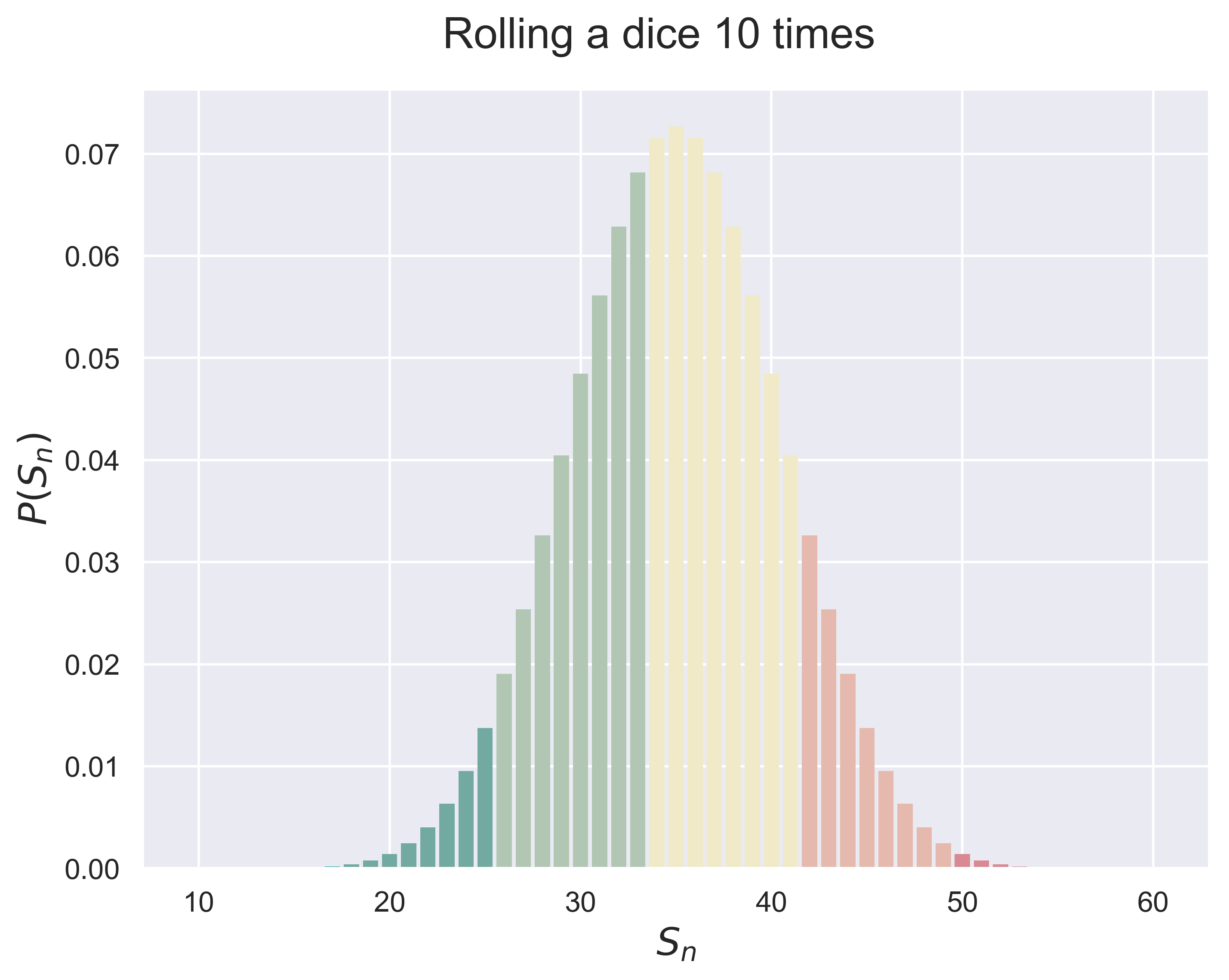
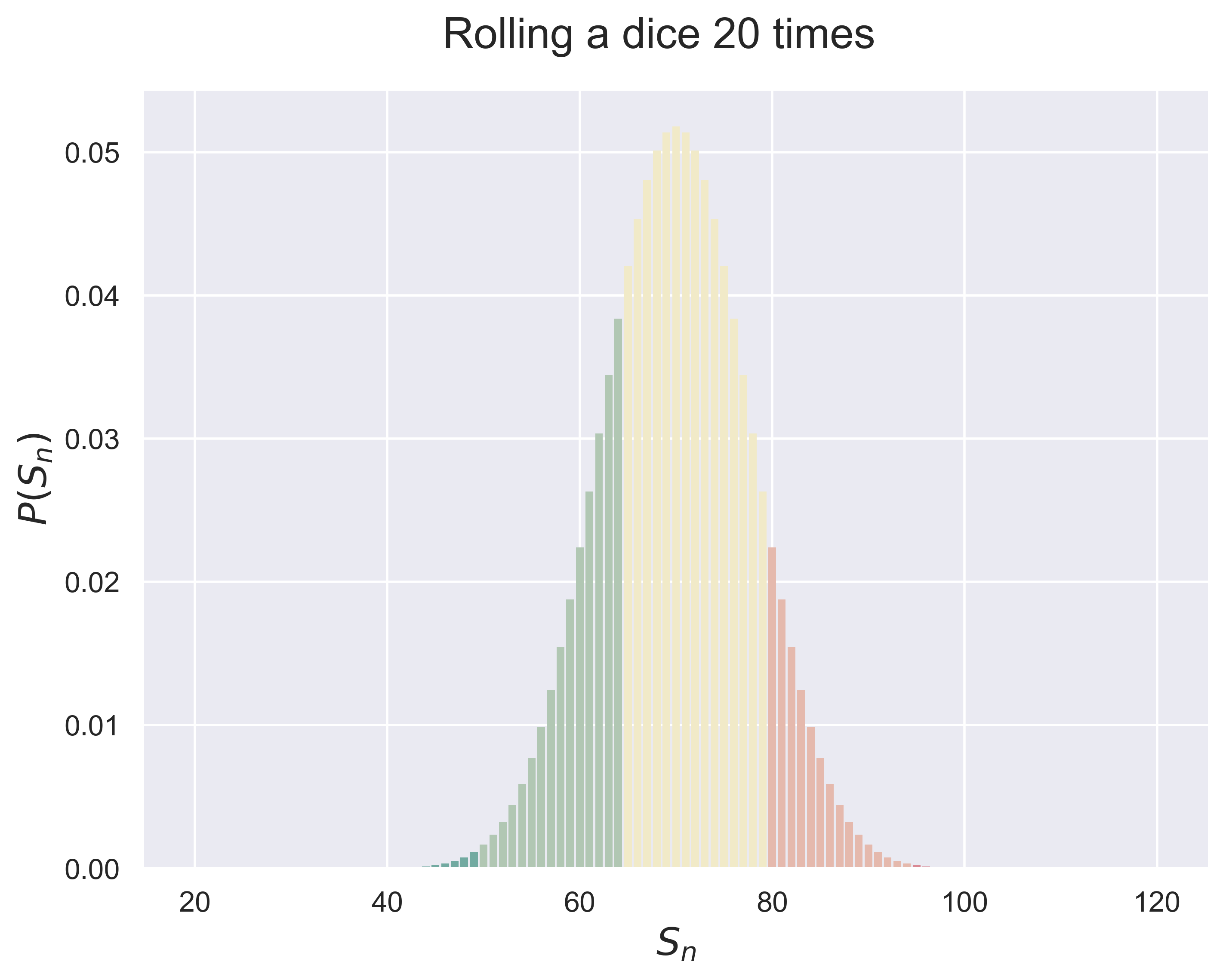
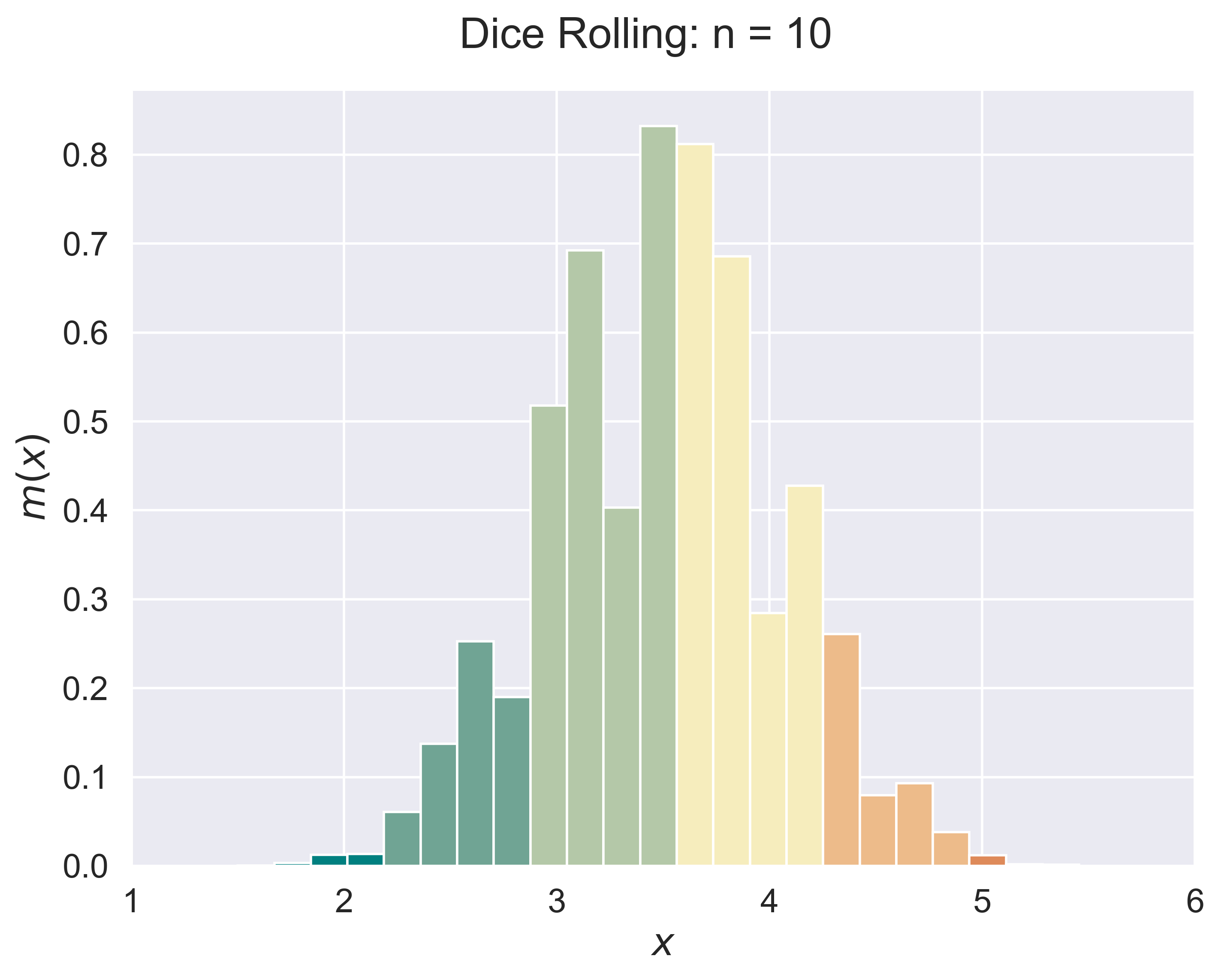
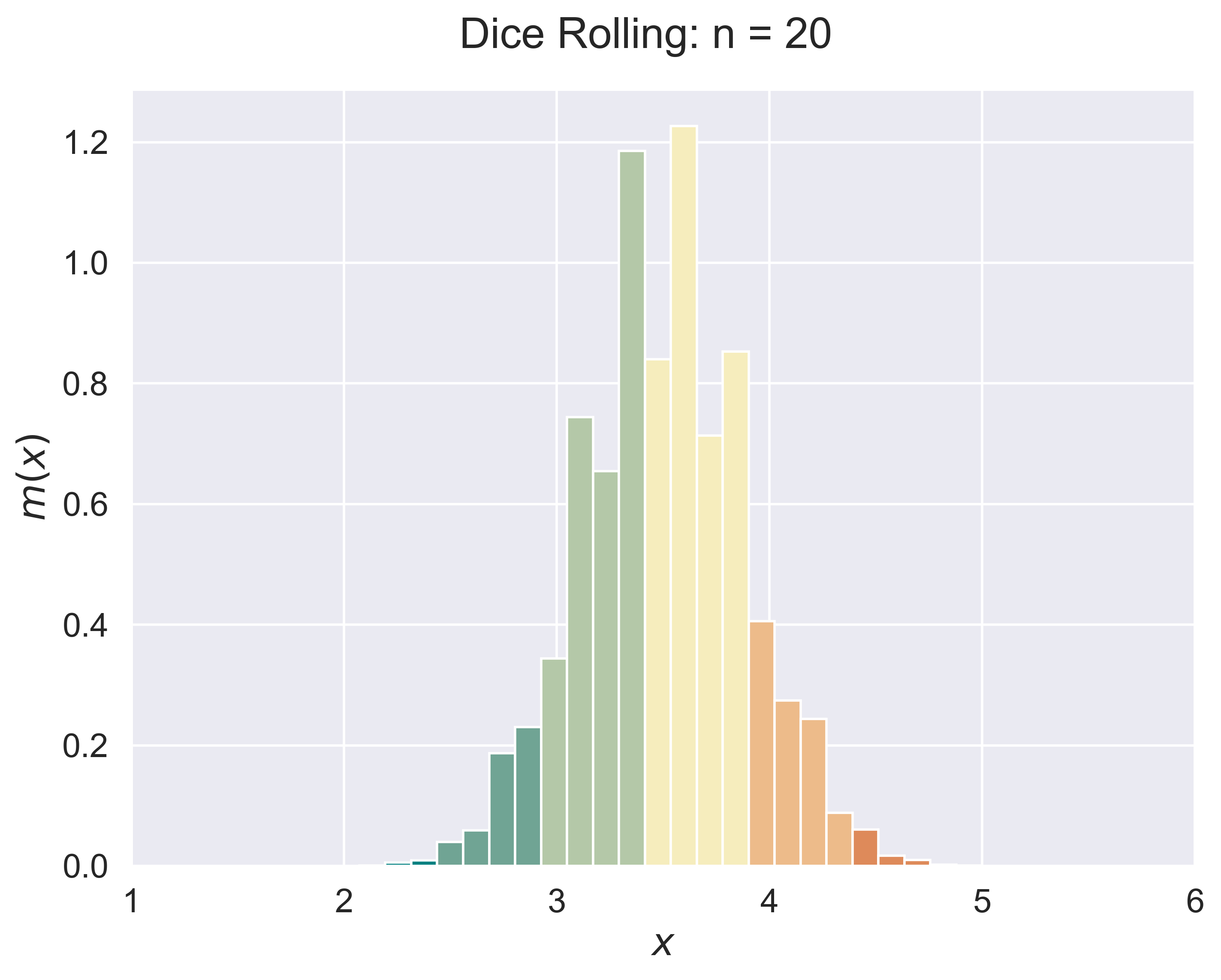
Roll a dice $n$ times.
dices(n = 10)
figure_dices(n = 5, fsize = (8, 6), fs = 18)
-
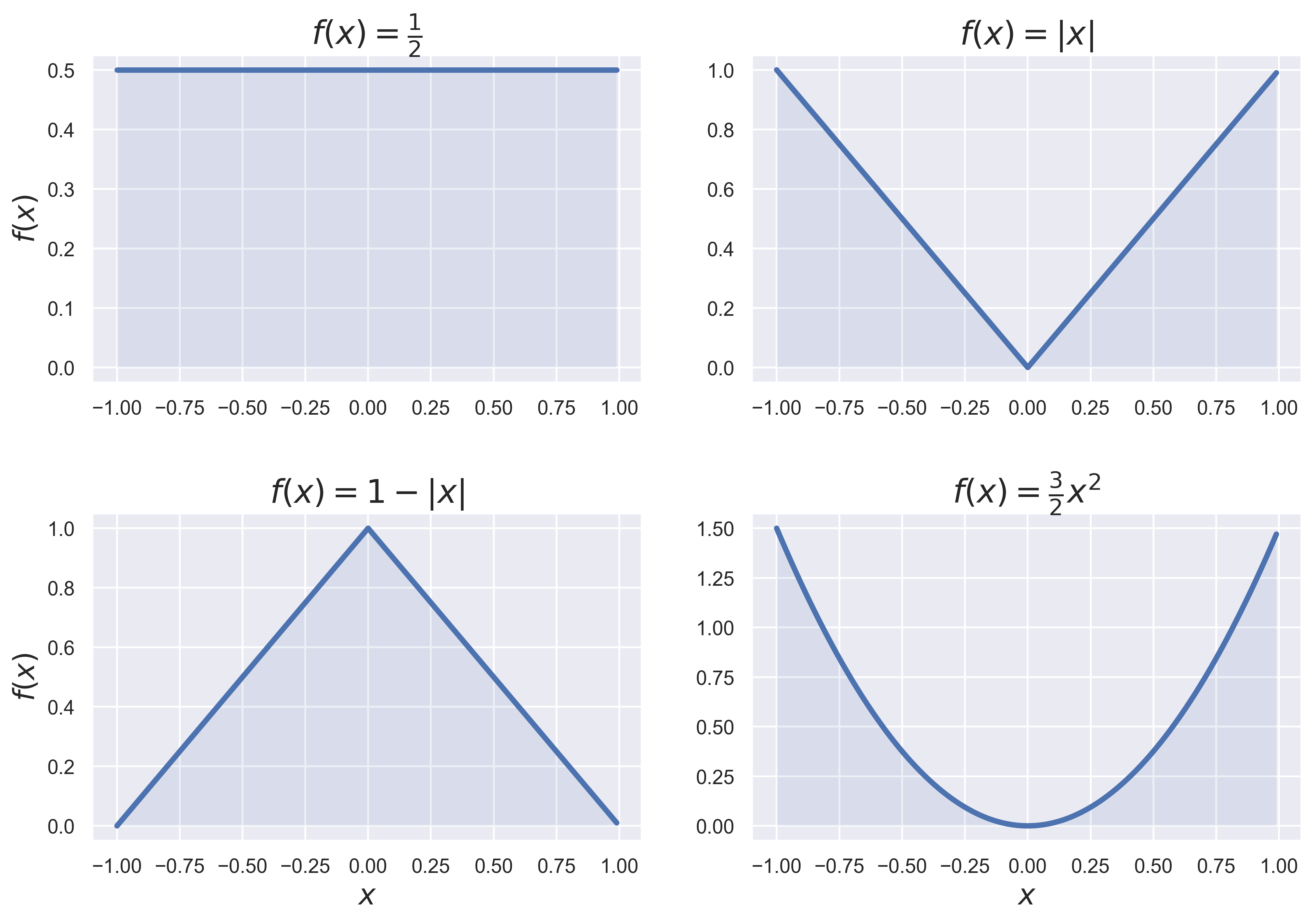
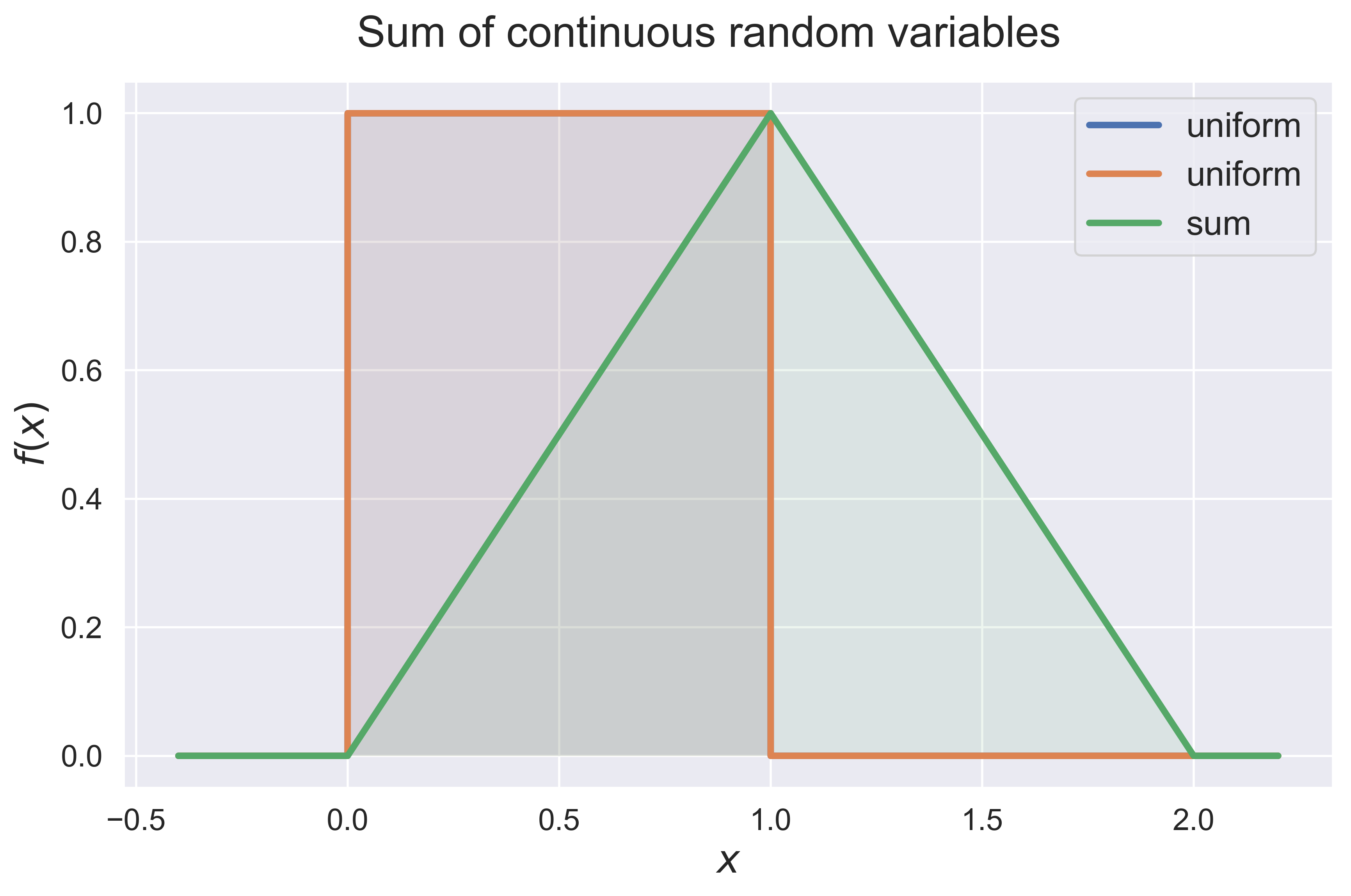
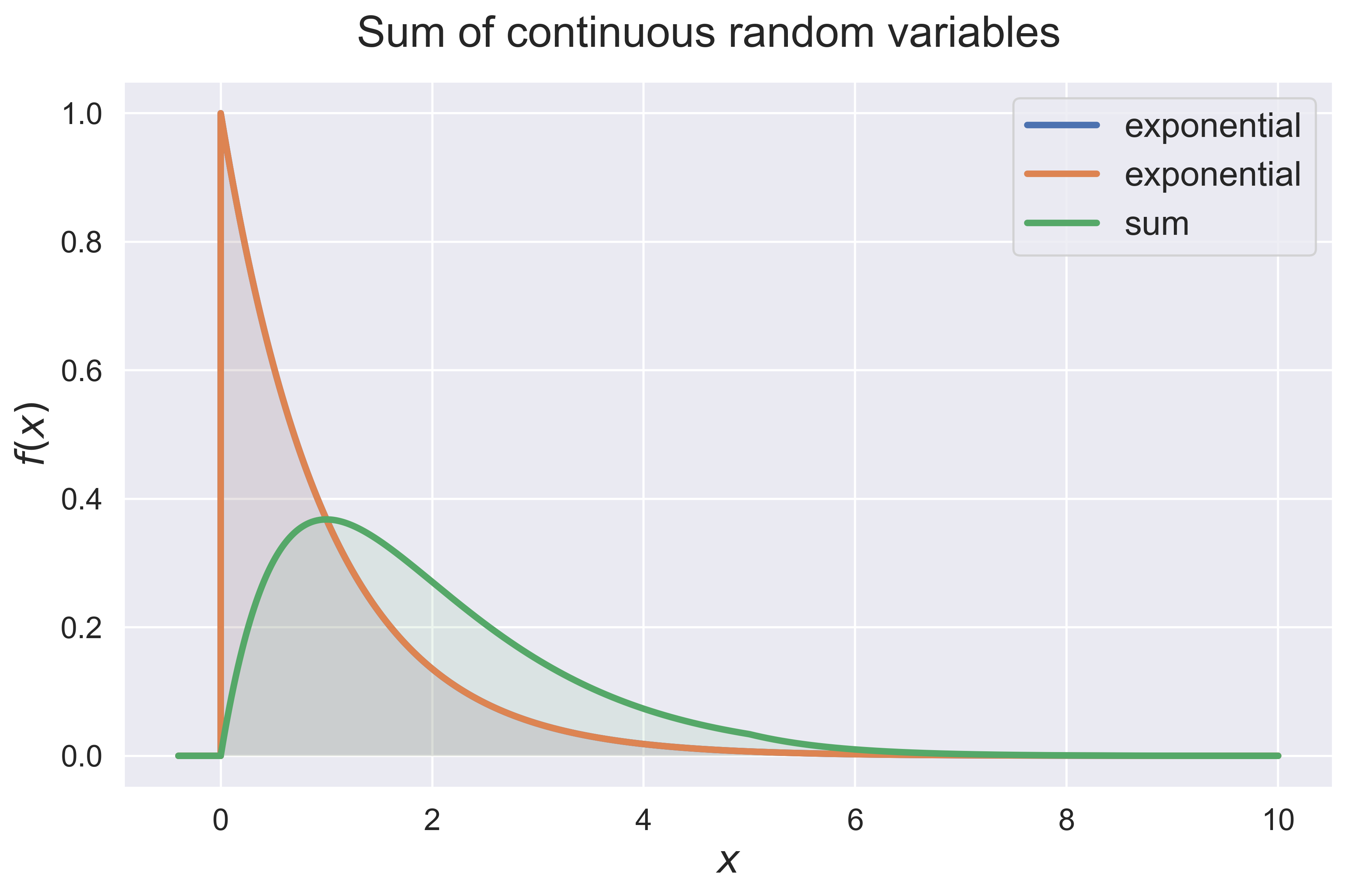
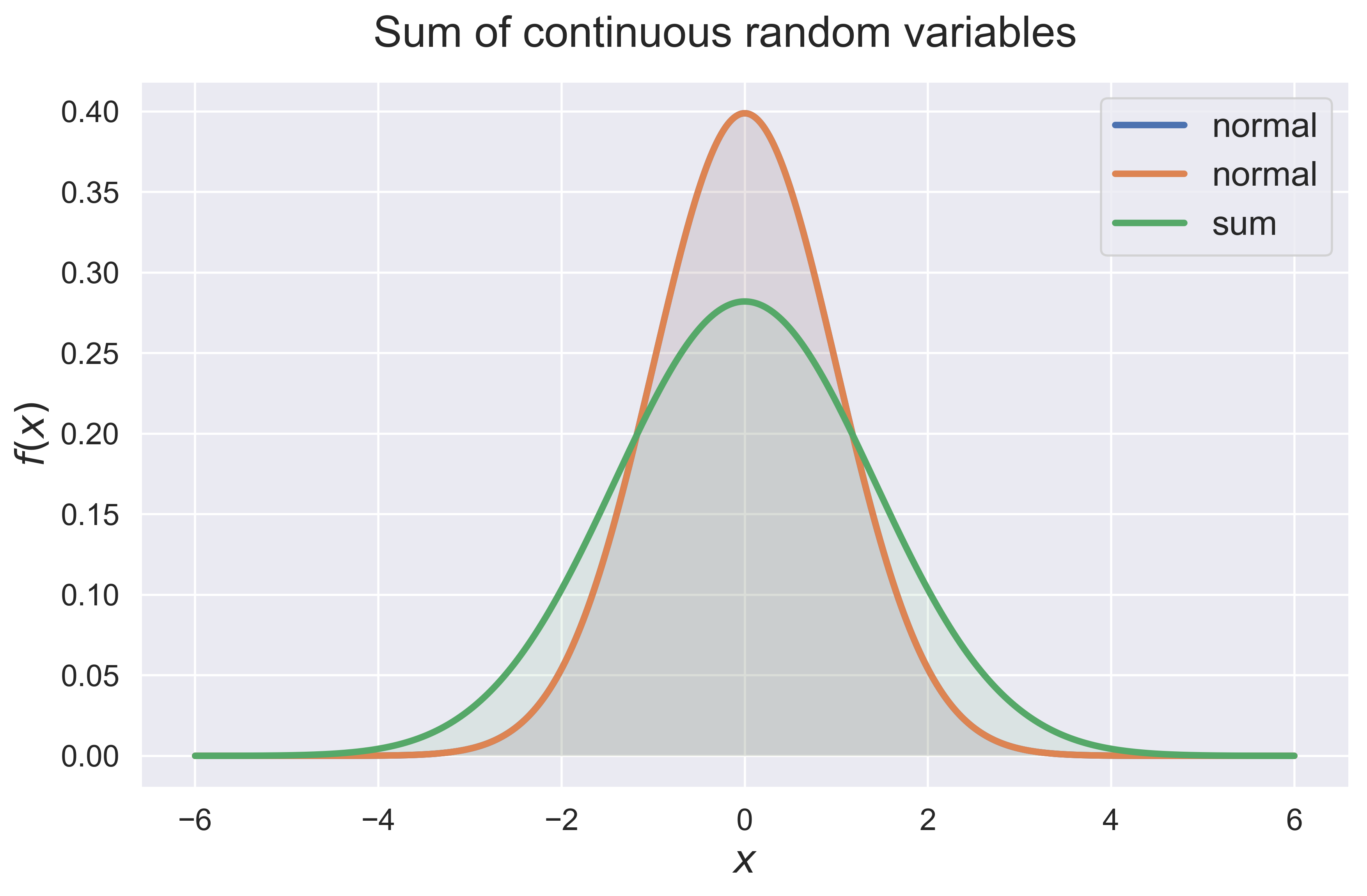
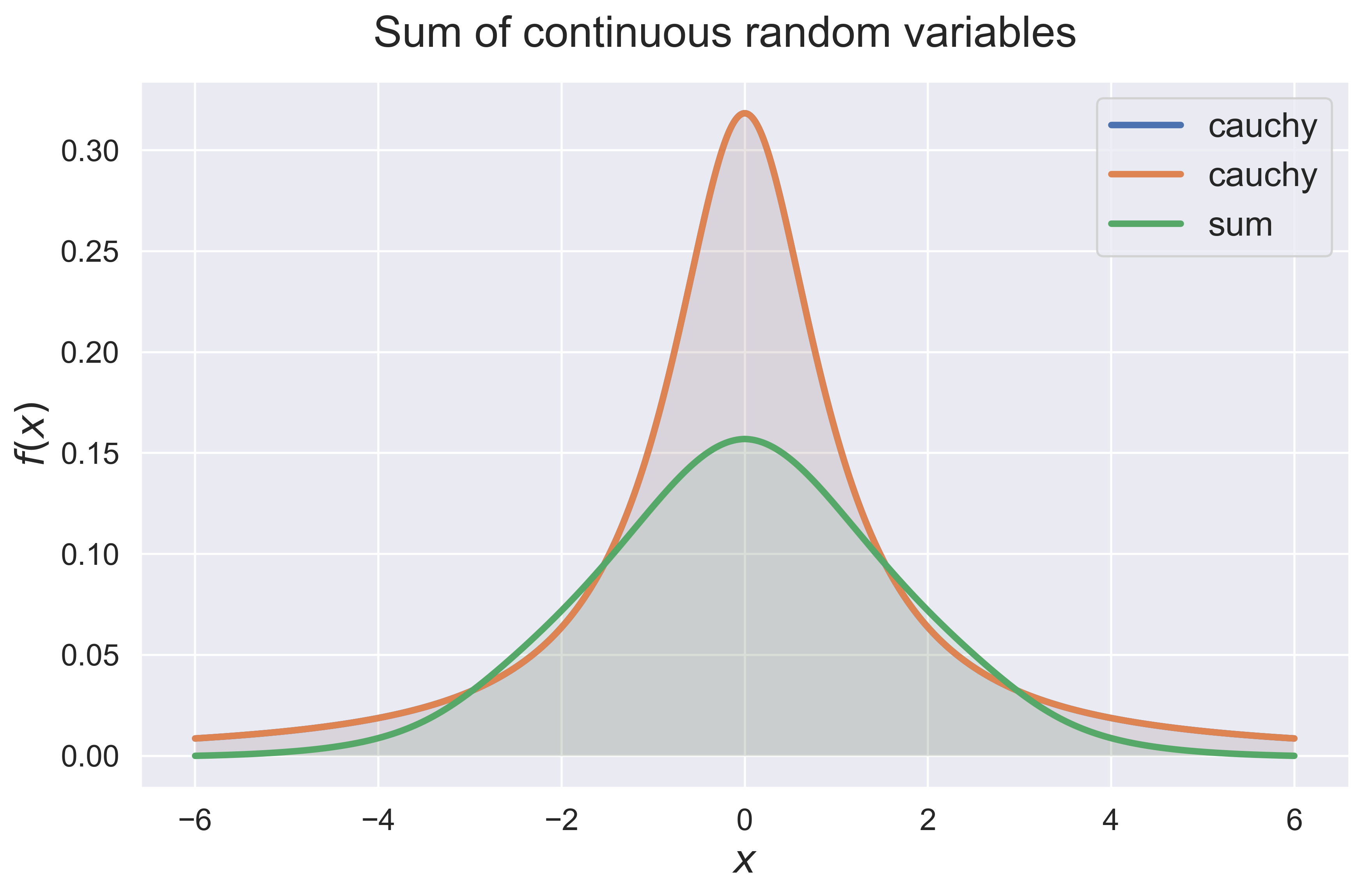
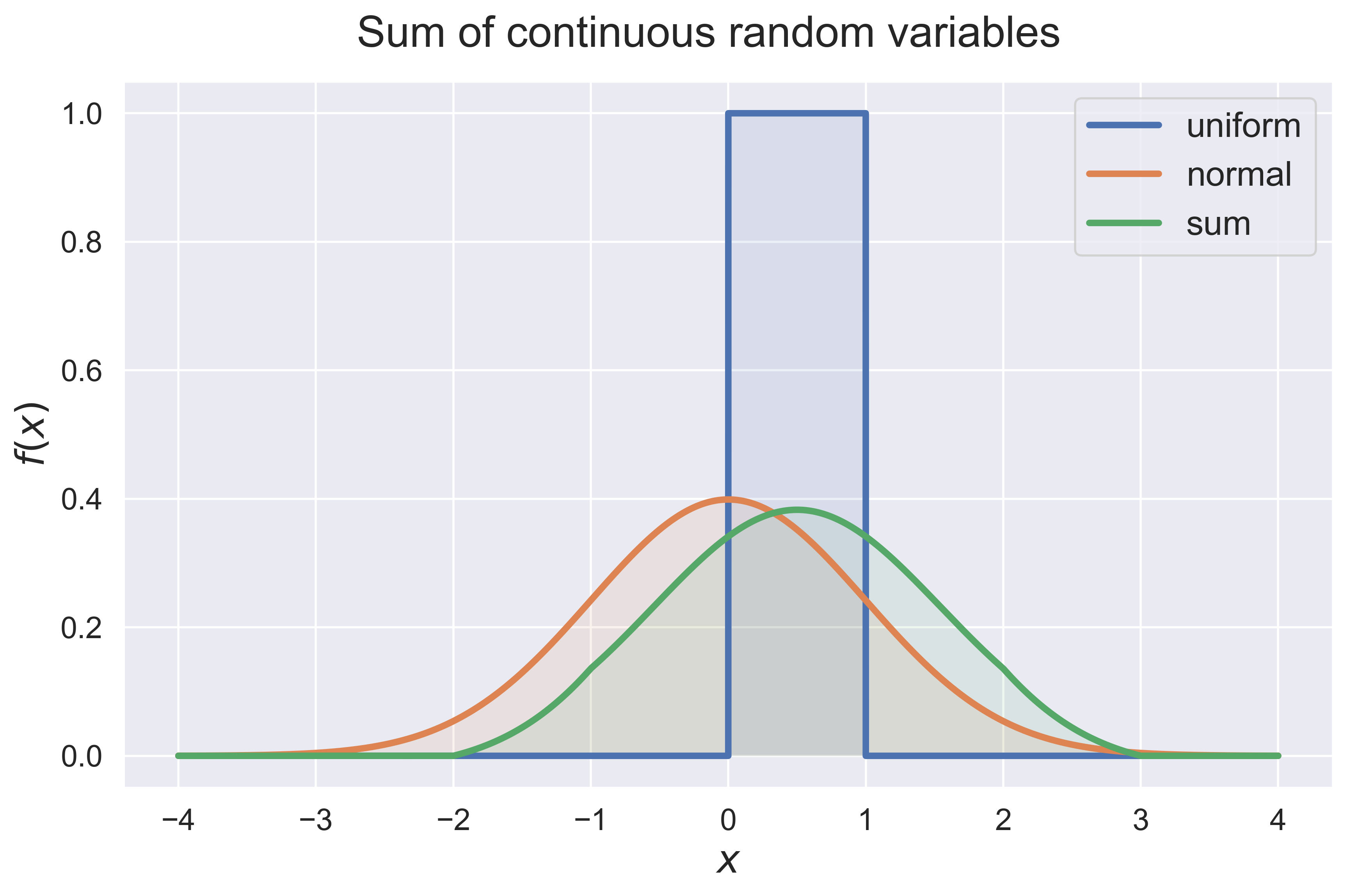
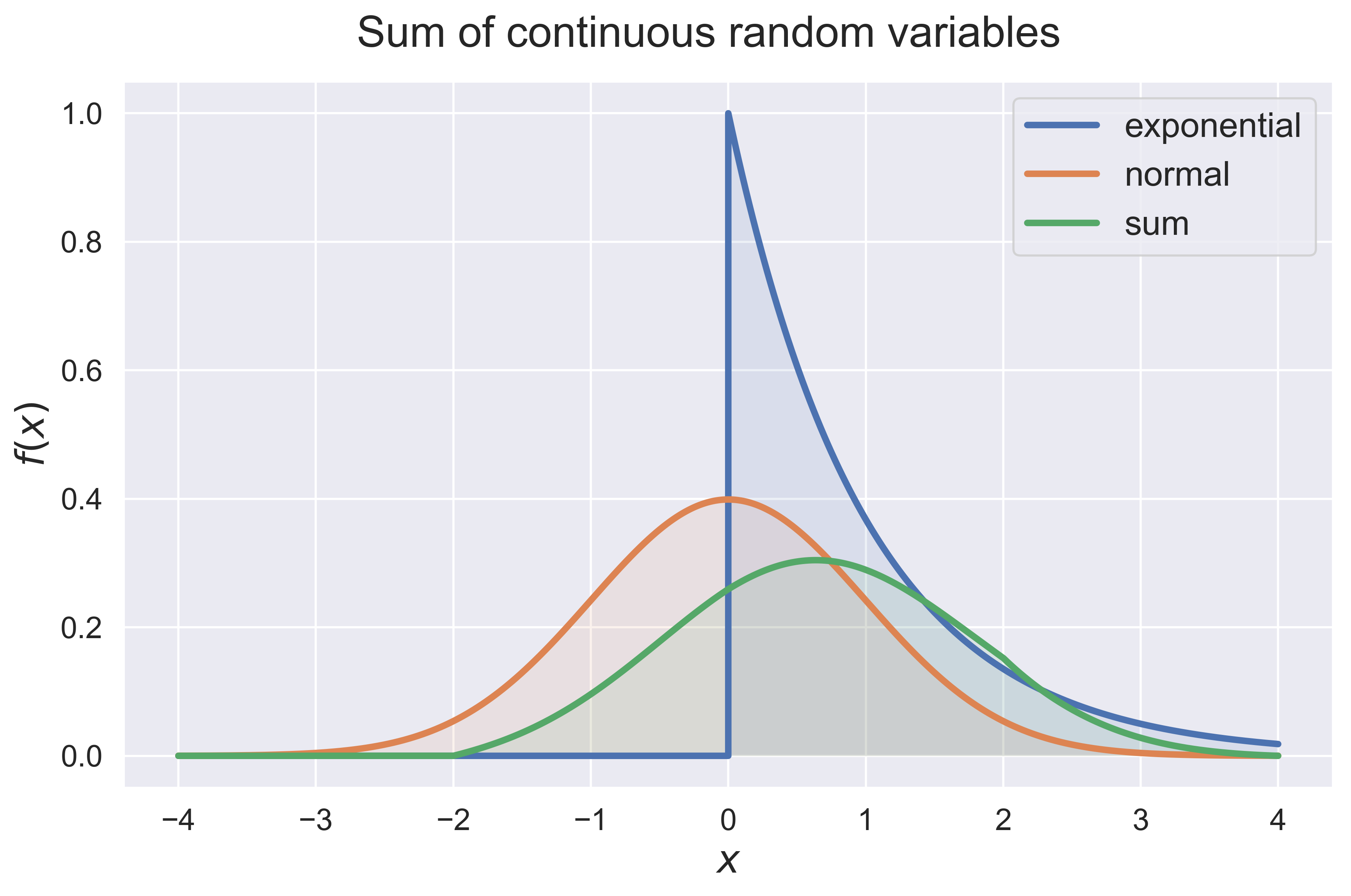
Sum of Independent Random Variables.
convolution(dist_1 = 'uniform', dist_2 = 'normal', interval = [-3, 3])
figure_convolution(dist_1 = 'uniform', dist_2 = 'uniform', interval = [-0.2, 1.1], fsize = (10, 6), fs = 20)
Slides 0819
-
Law of Large Numbers for a Discrete Random Variable
LLN_experiment(experiment = "coin", n = 10, p = 0.5)
LLN(experiment = 'coin', n = 10, p = 0.5)
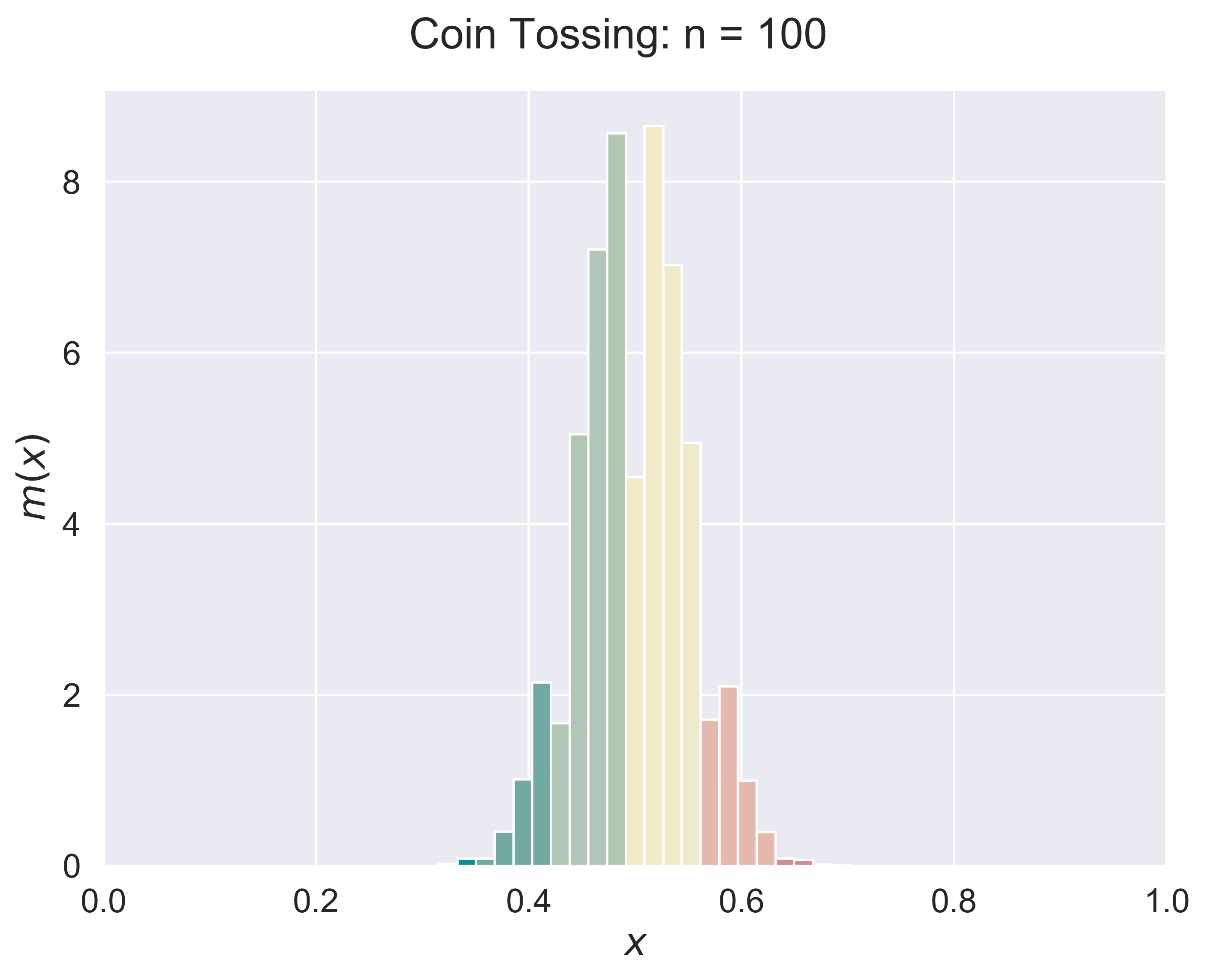
figure_LLN(experiment = 'coin', n = 10, p = 0.5, fsize = (8, 6), fs = 18)
Coin Tossing
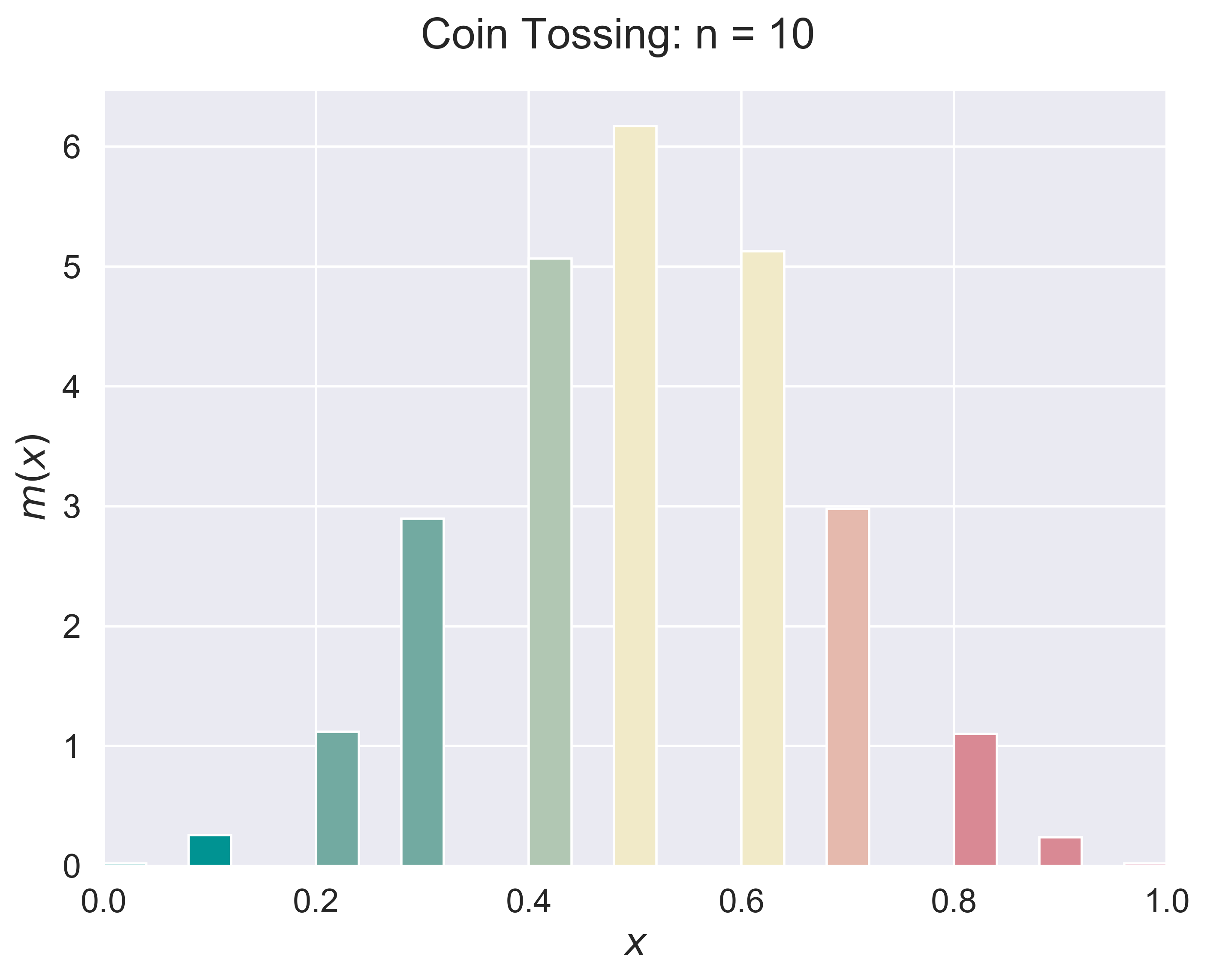 |
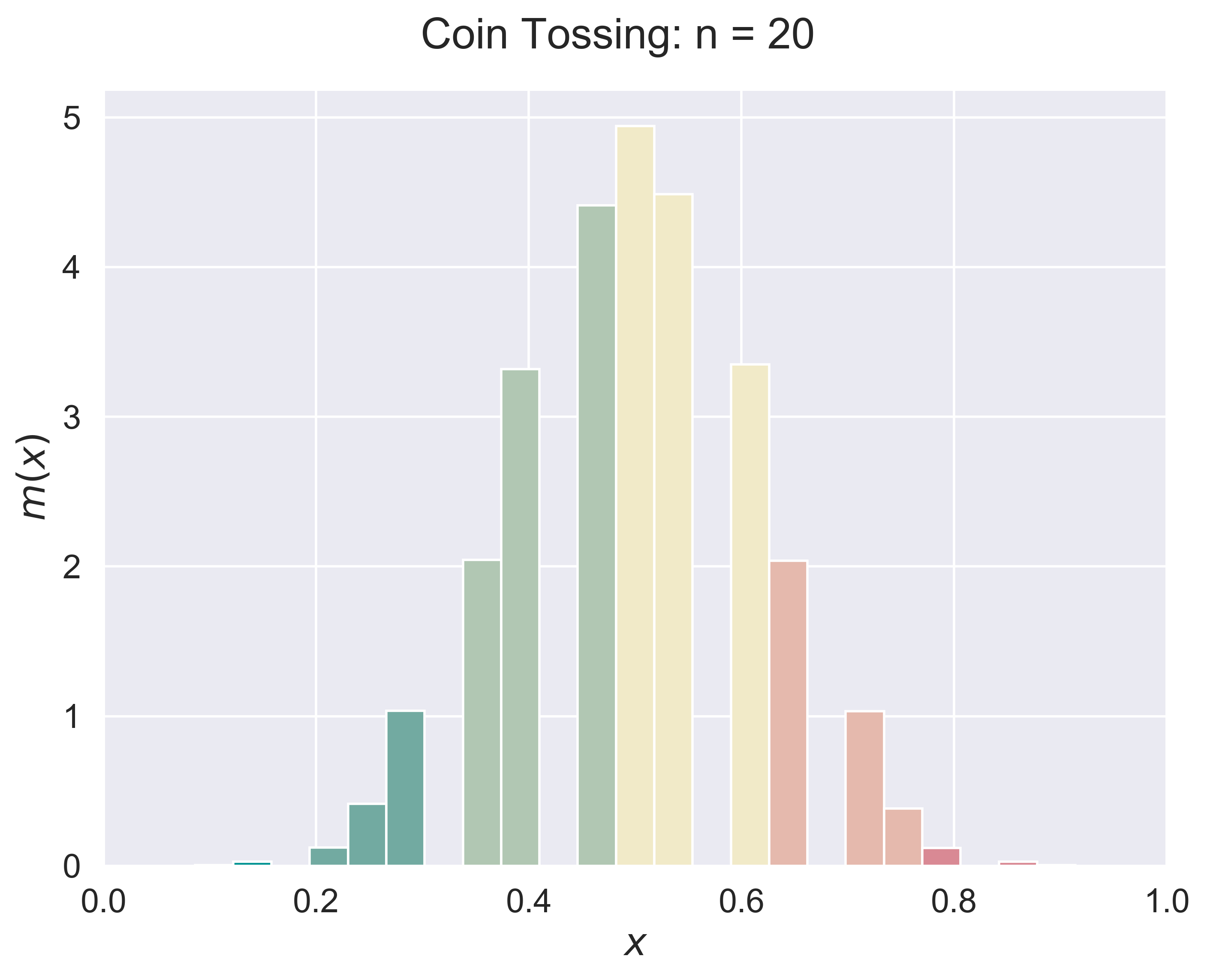 |
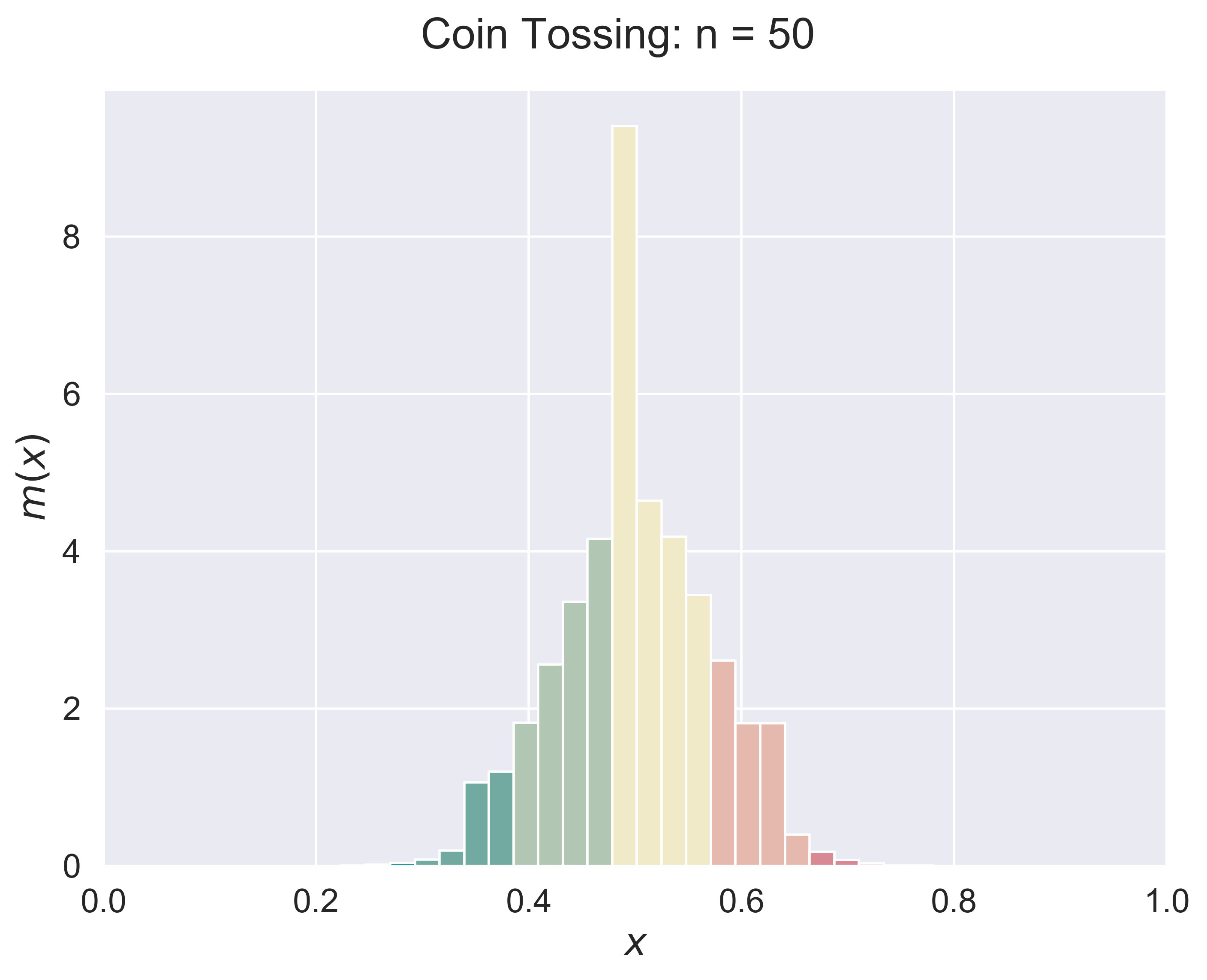 |
 |
</table>
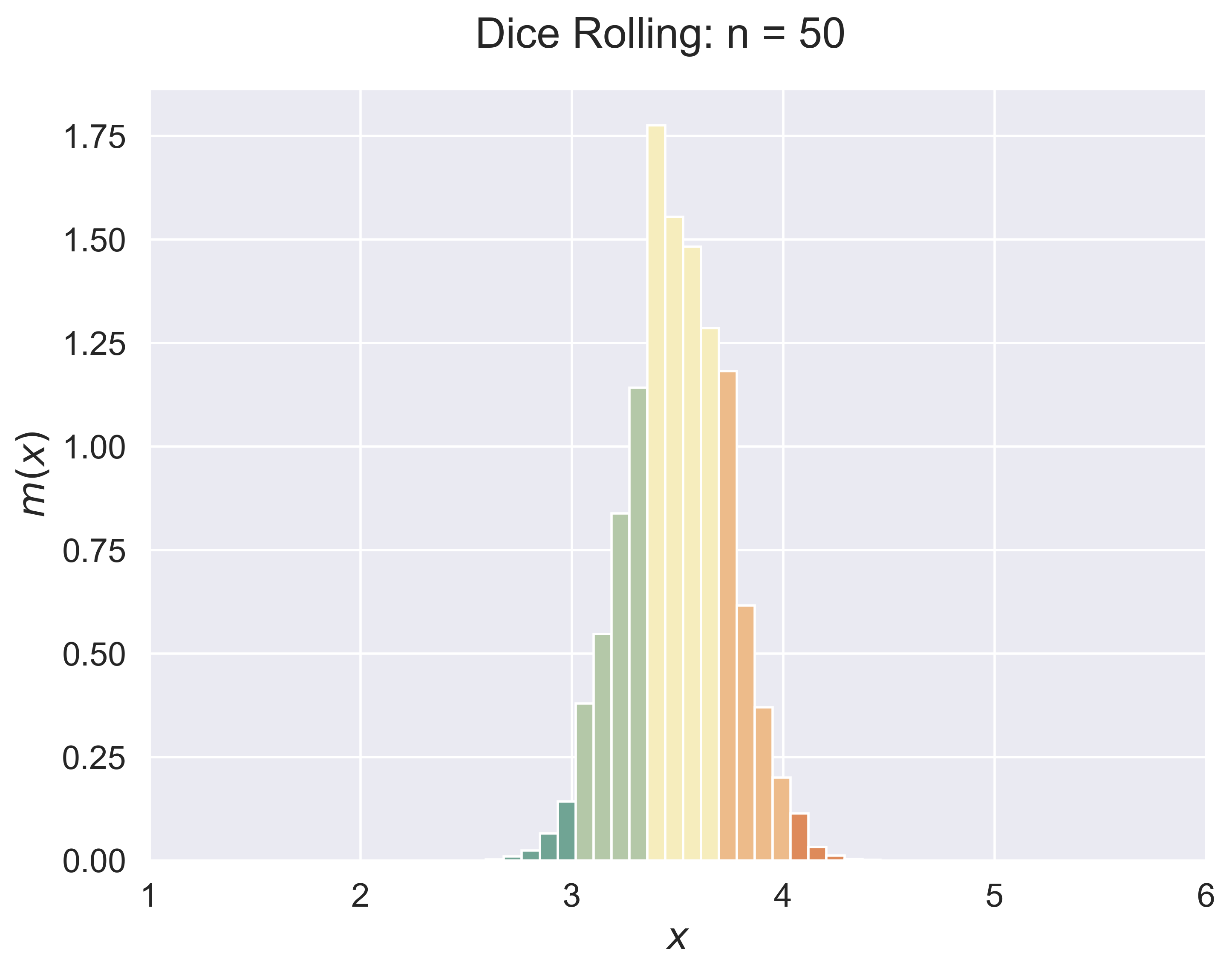
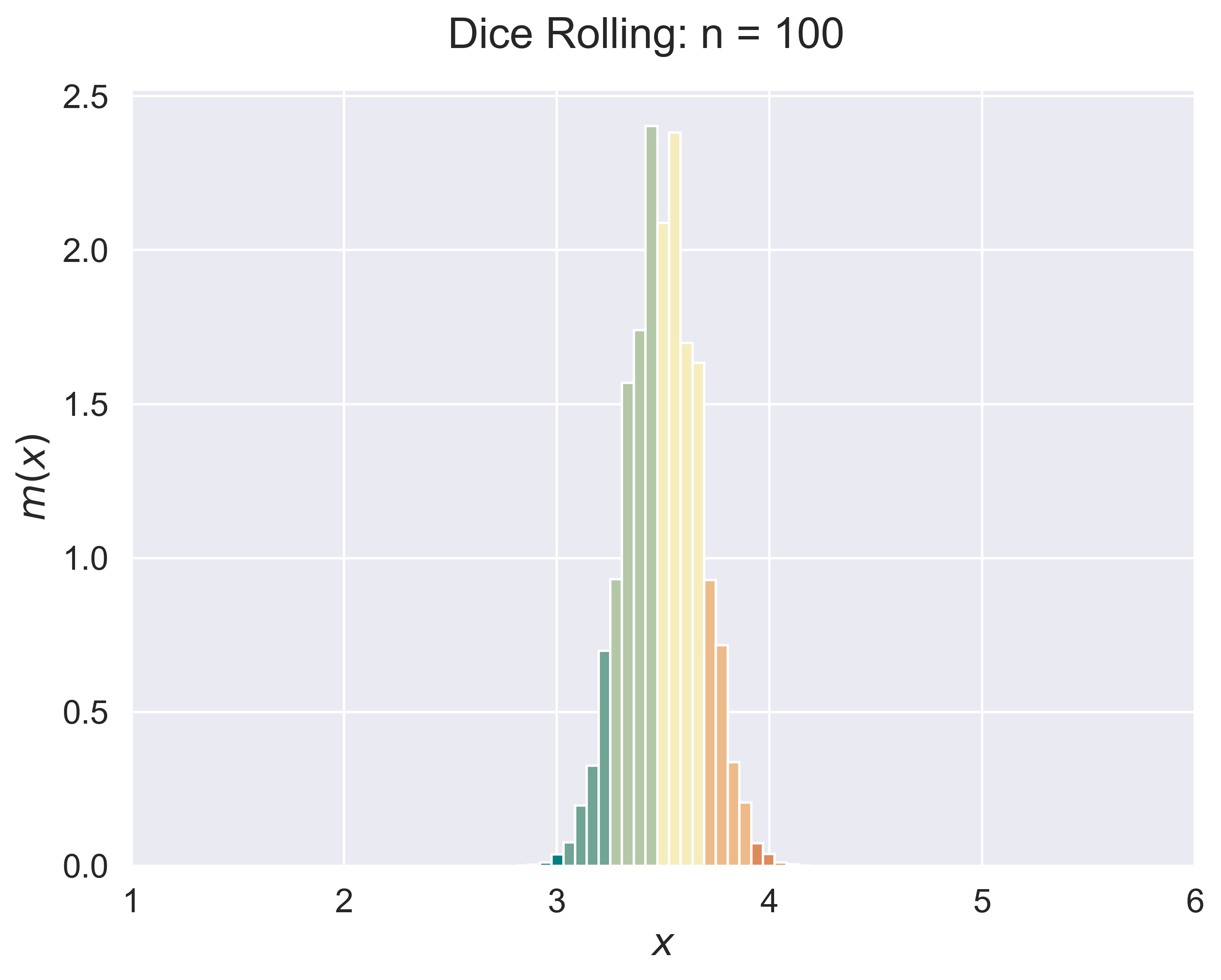
Dice Rolling
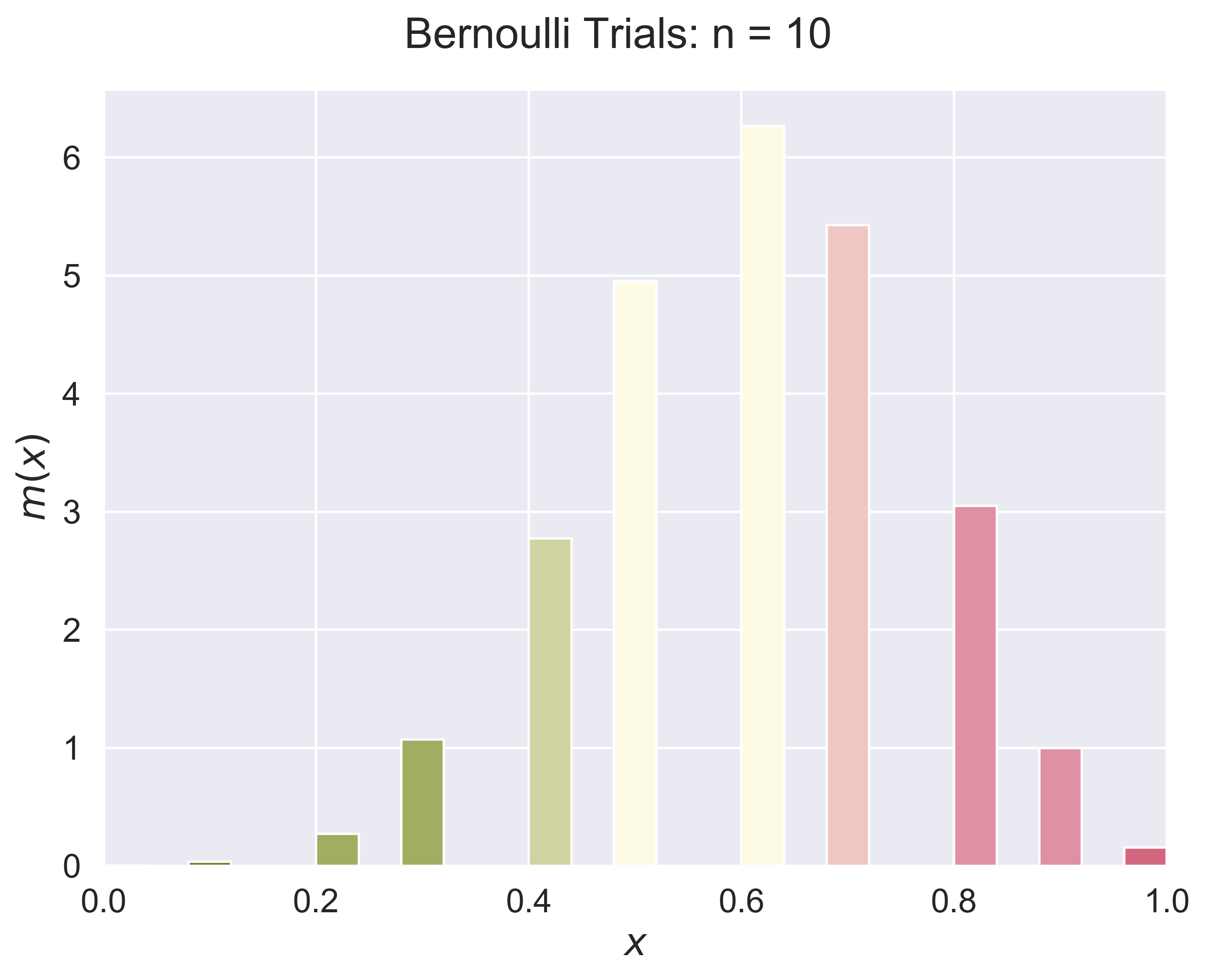
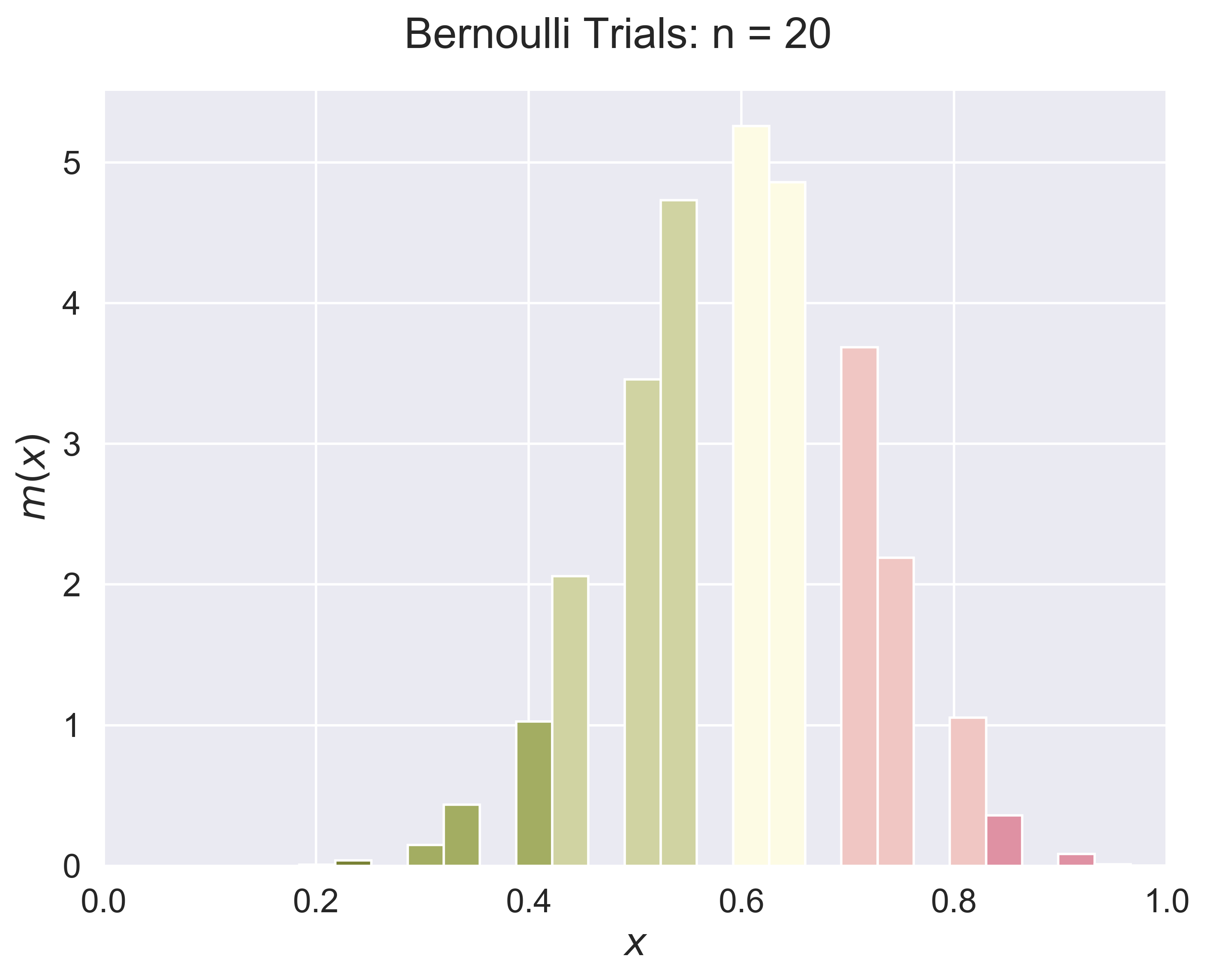
A General Bernoulli Trials Process
-
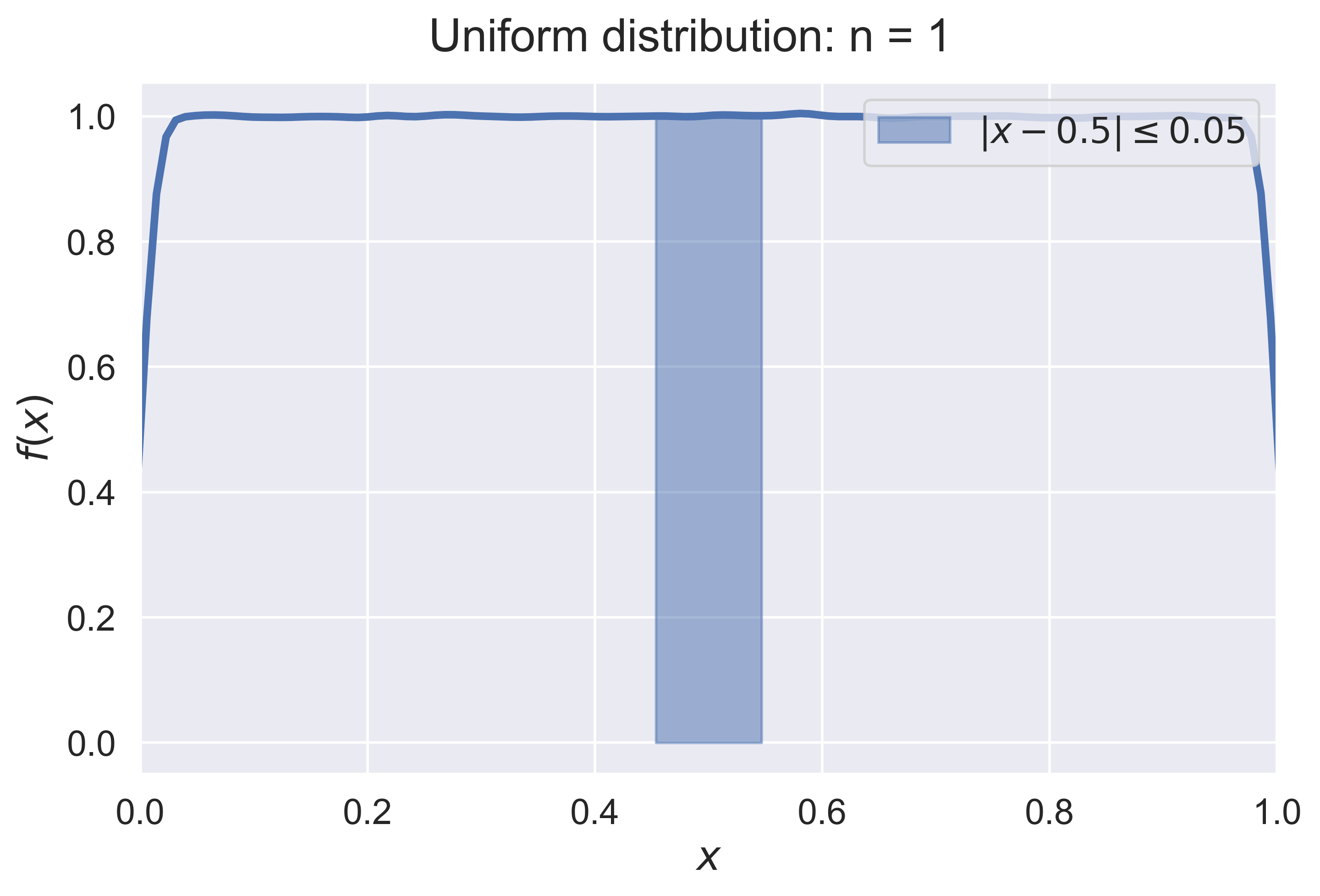
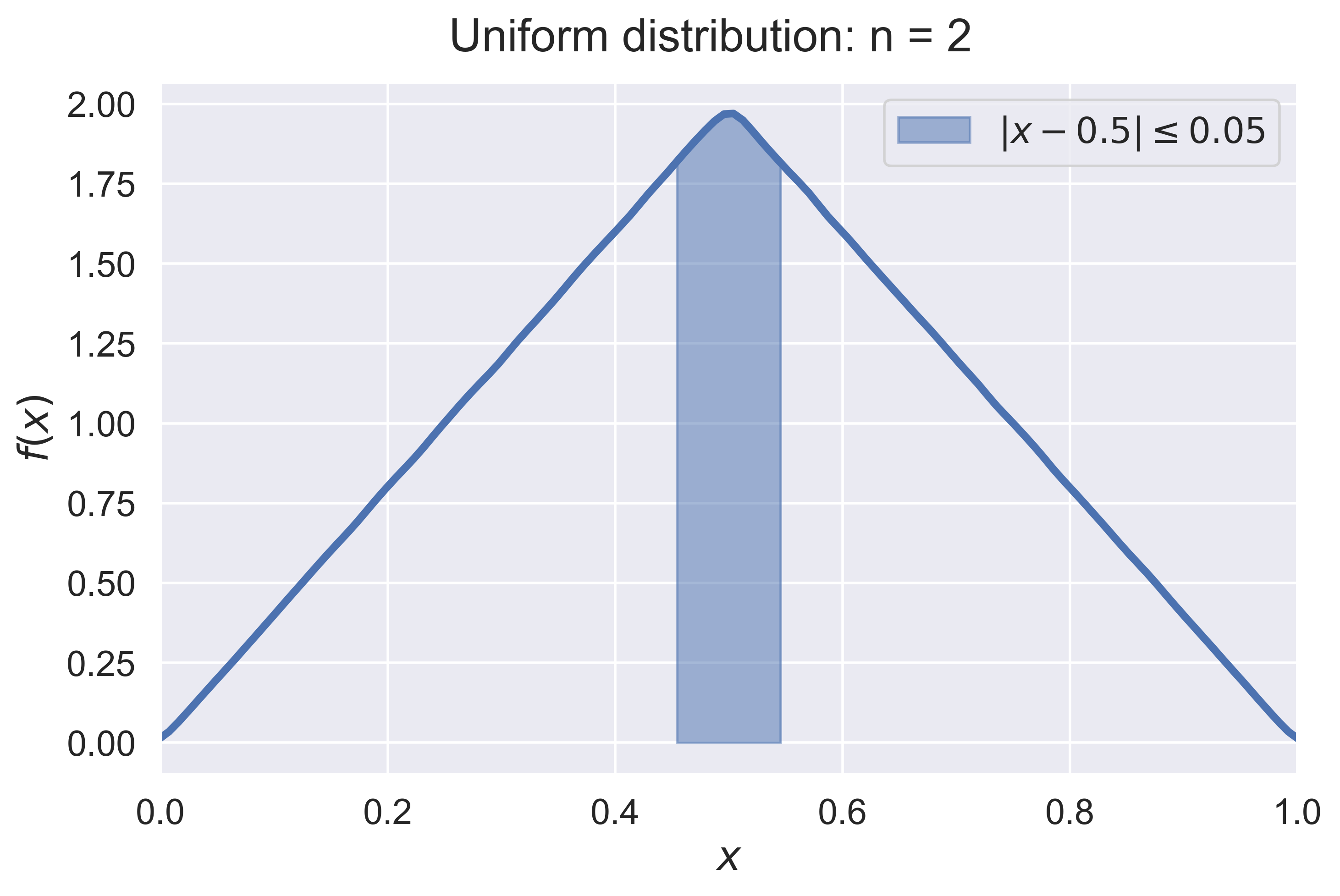
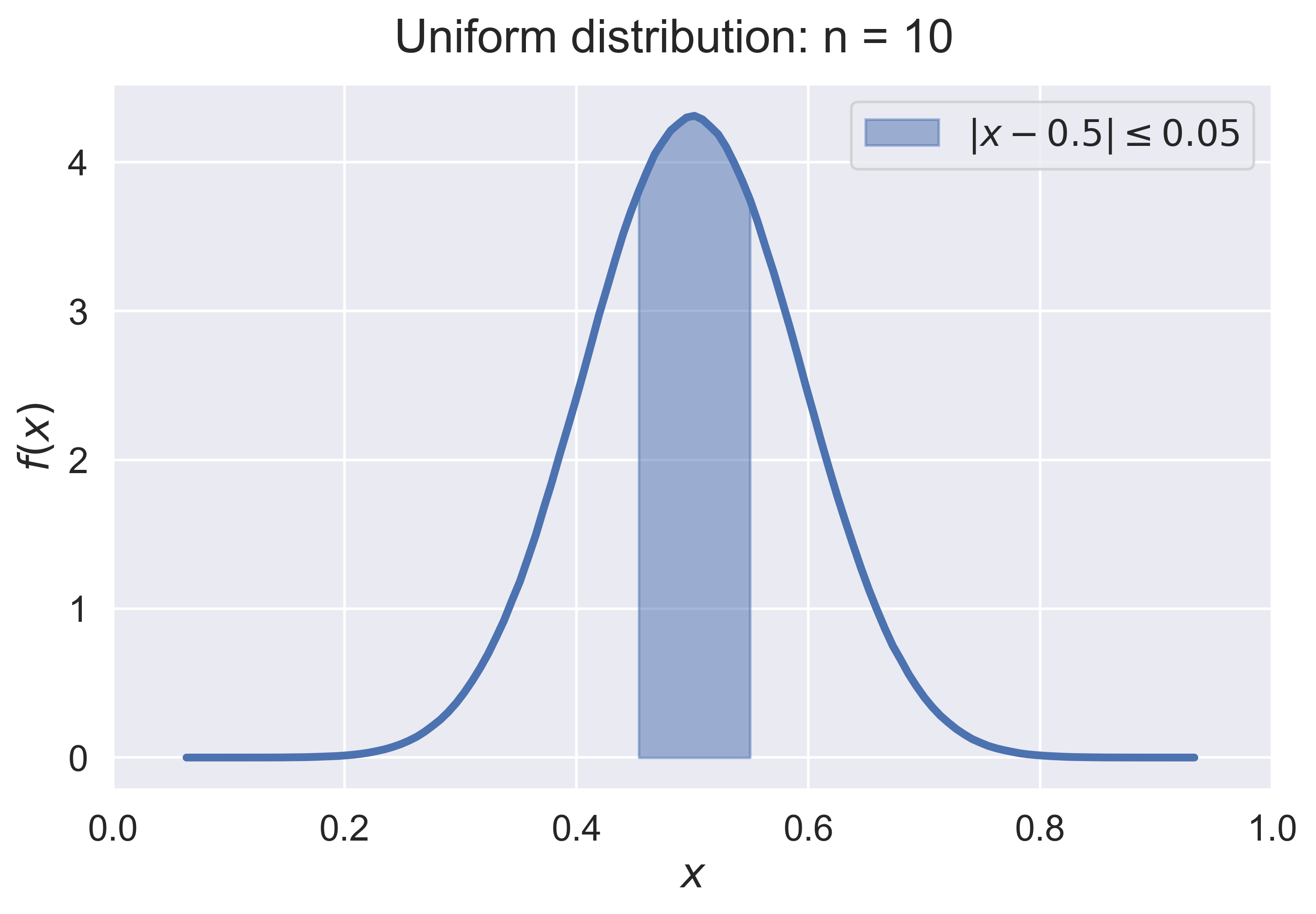
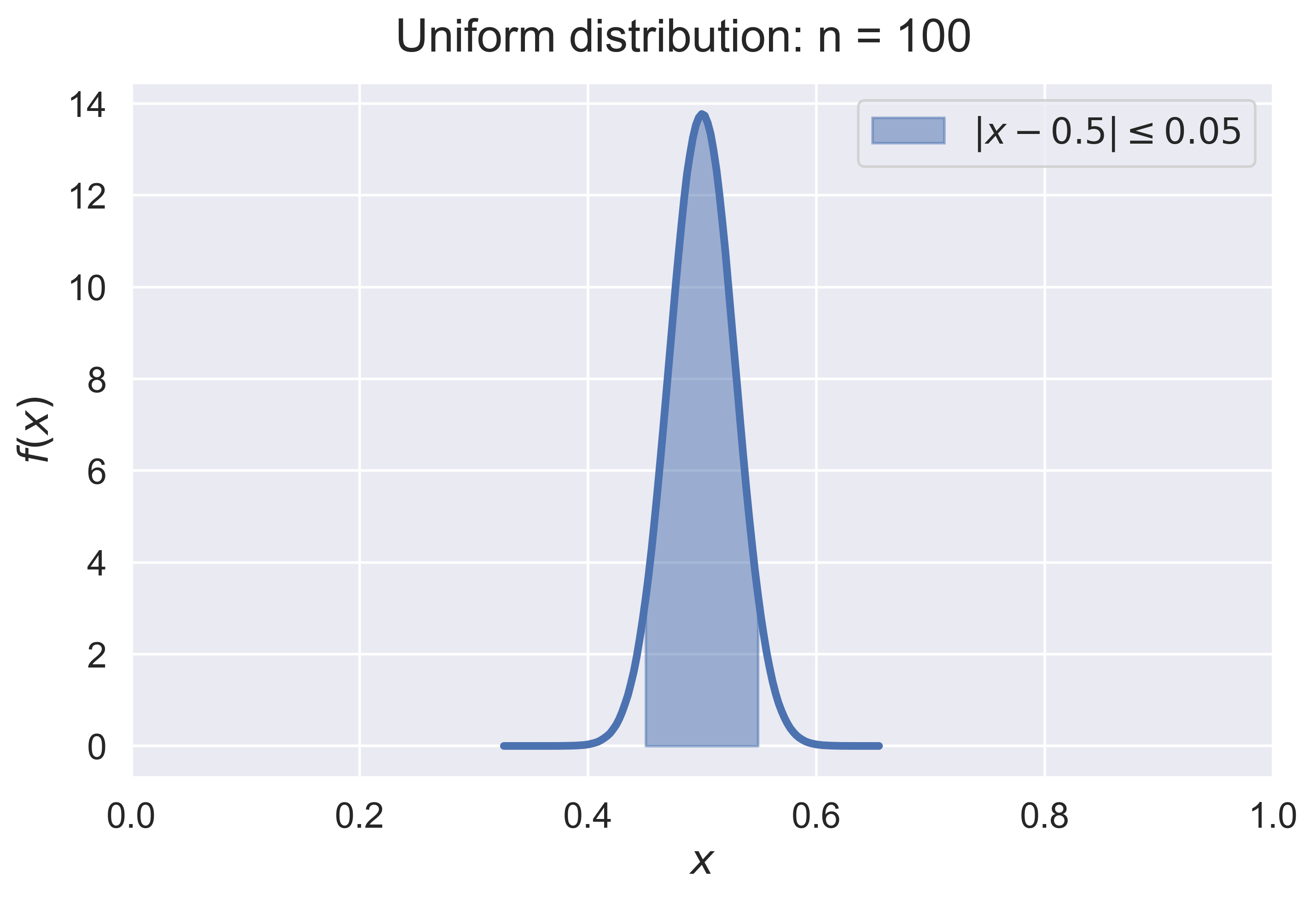
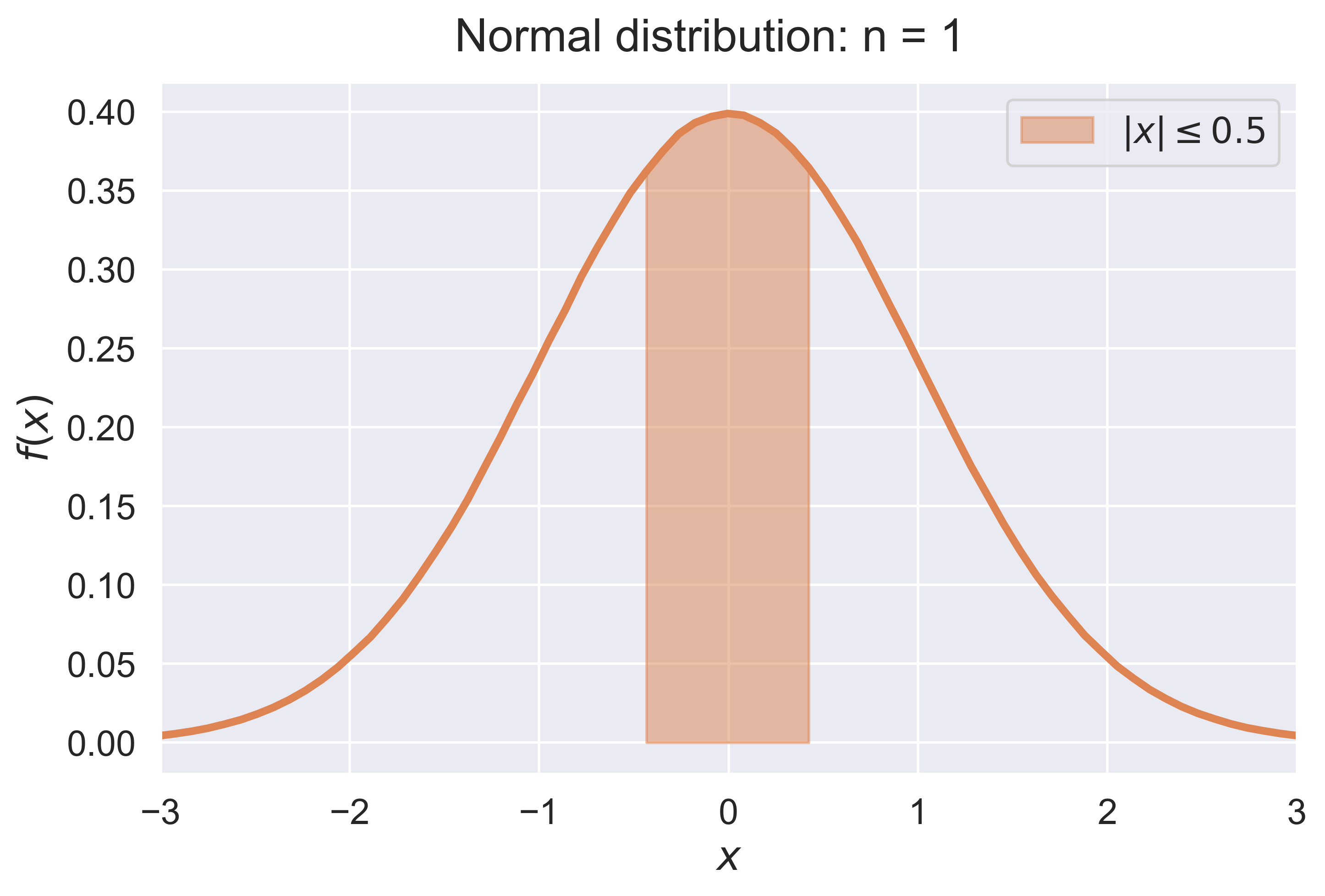
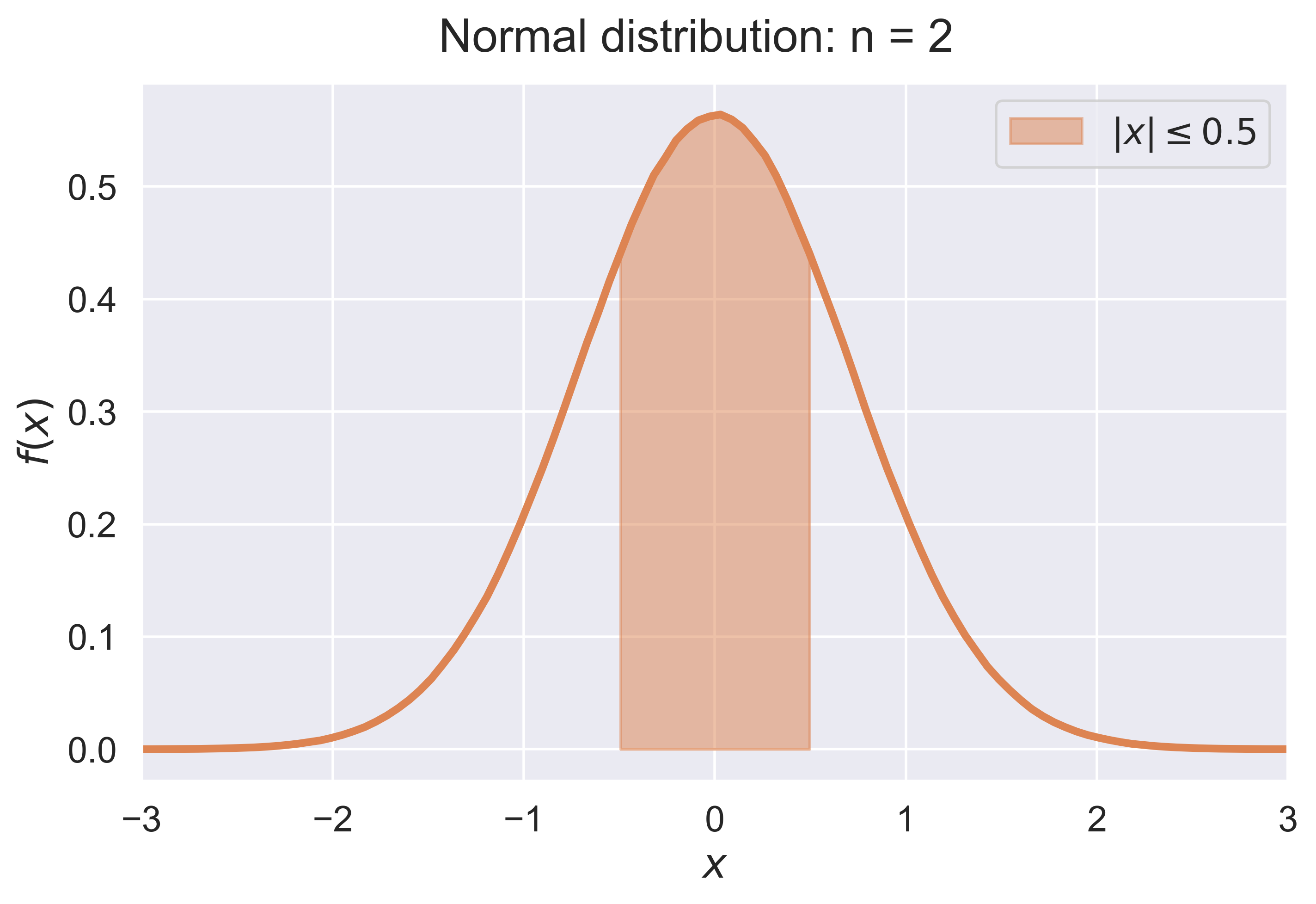
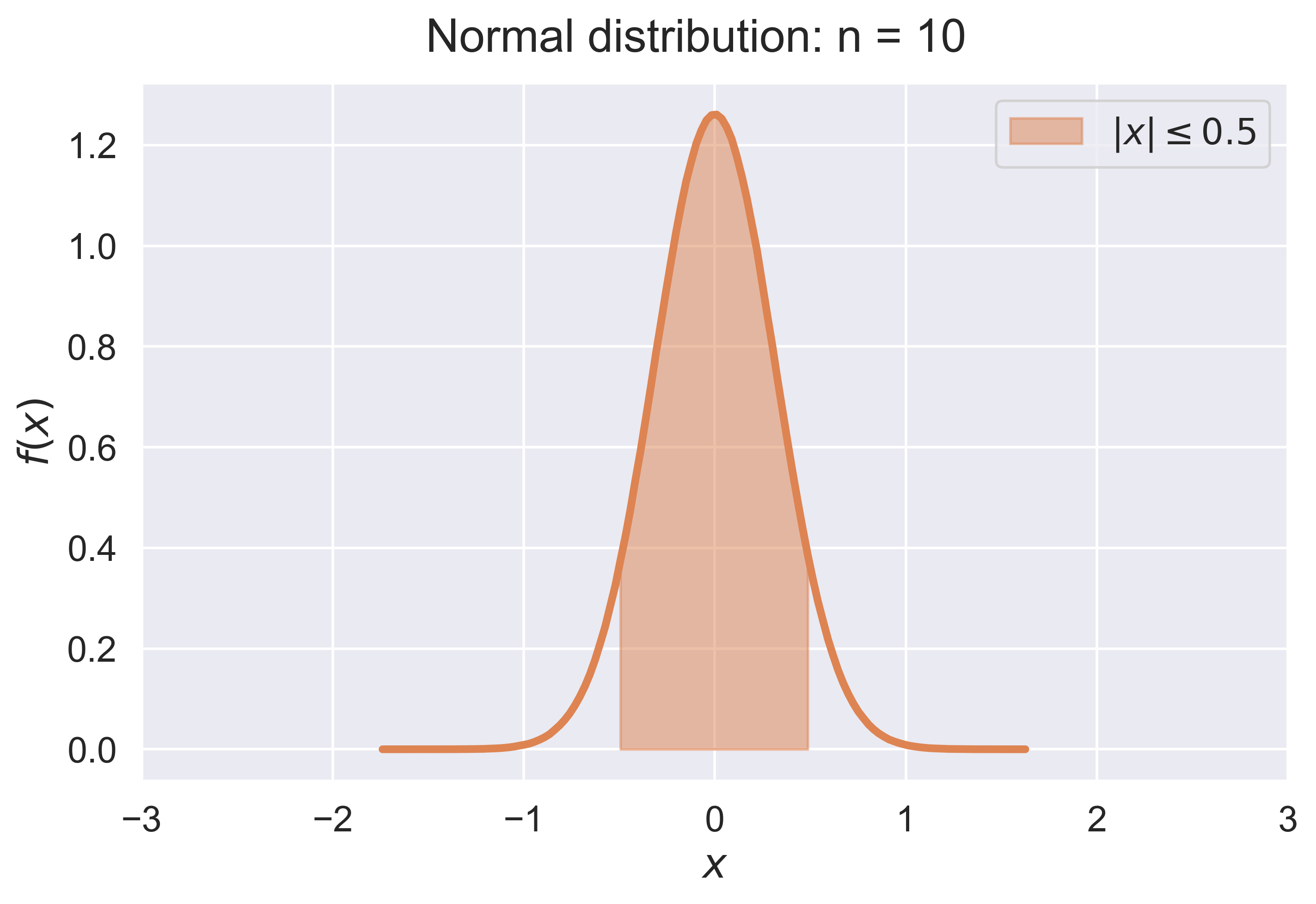
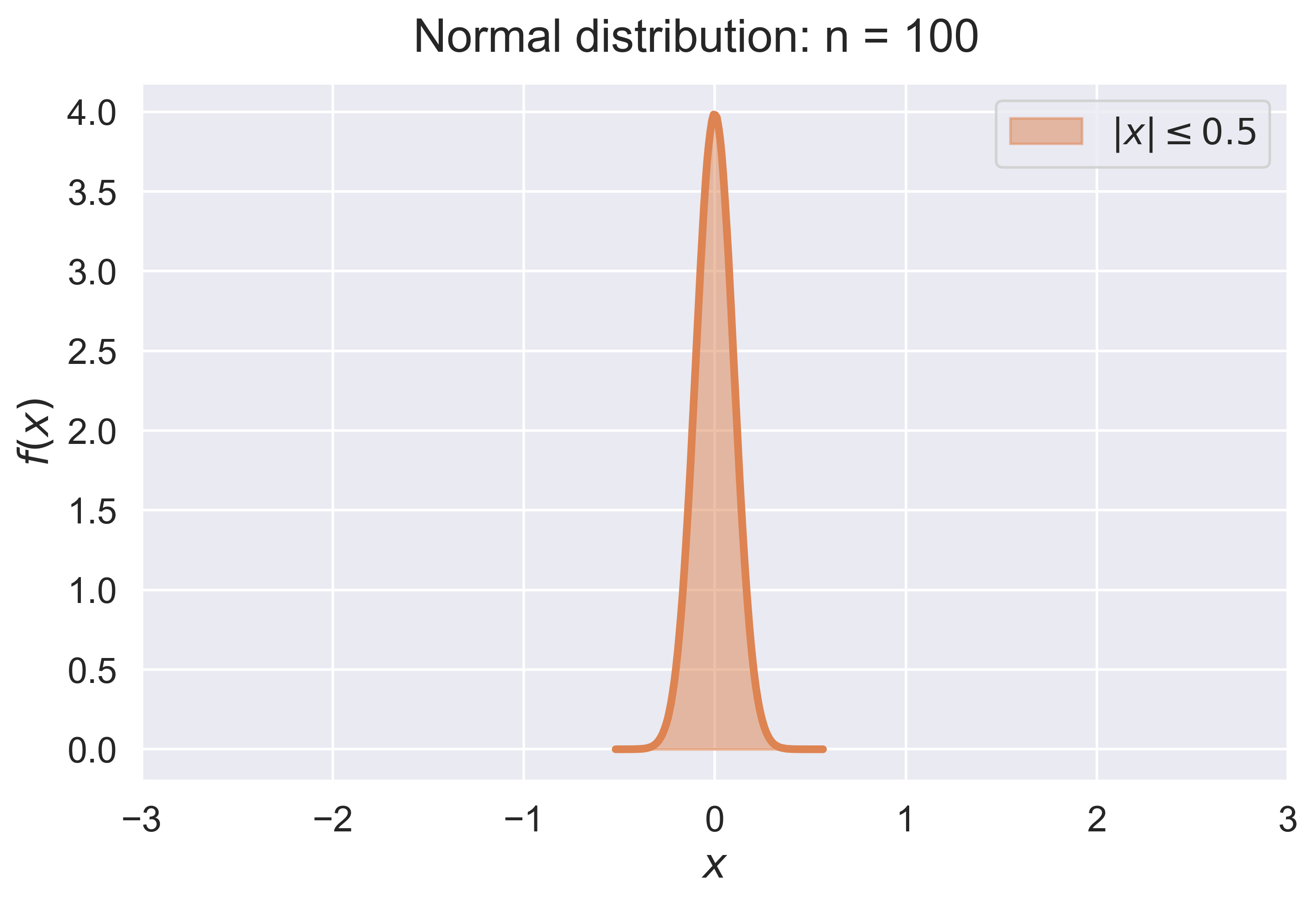
Law of Large Numbers for a Continuous Random Variable
LLN_experiment_continuous(experiment = "normal")
LLN_continuous(experiment = "normal", n = 10)
figure_LLN_continuous(experiment = 'normal', n = 10, fsize = (8, 5), fs = 18)
Unifrom Density
Normal Density
-
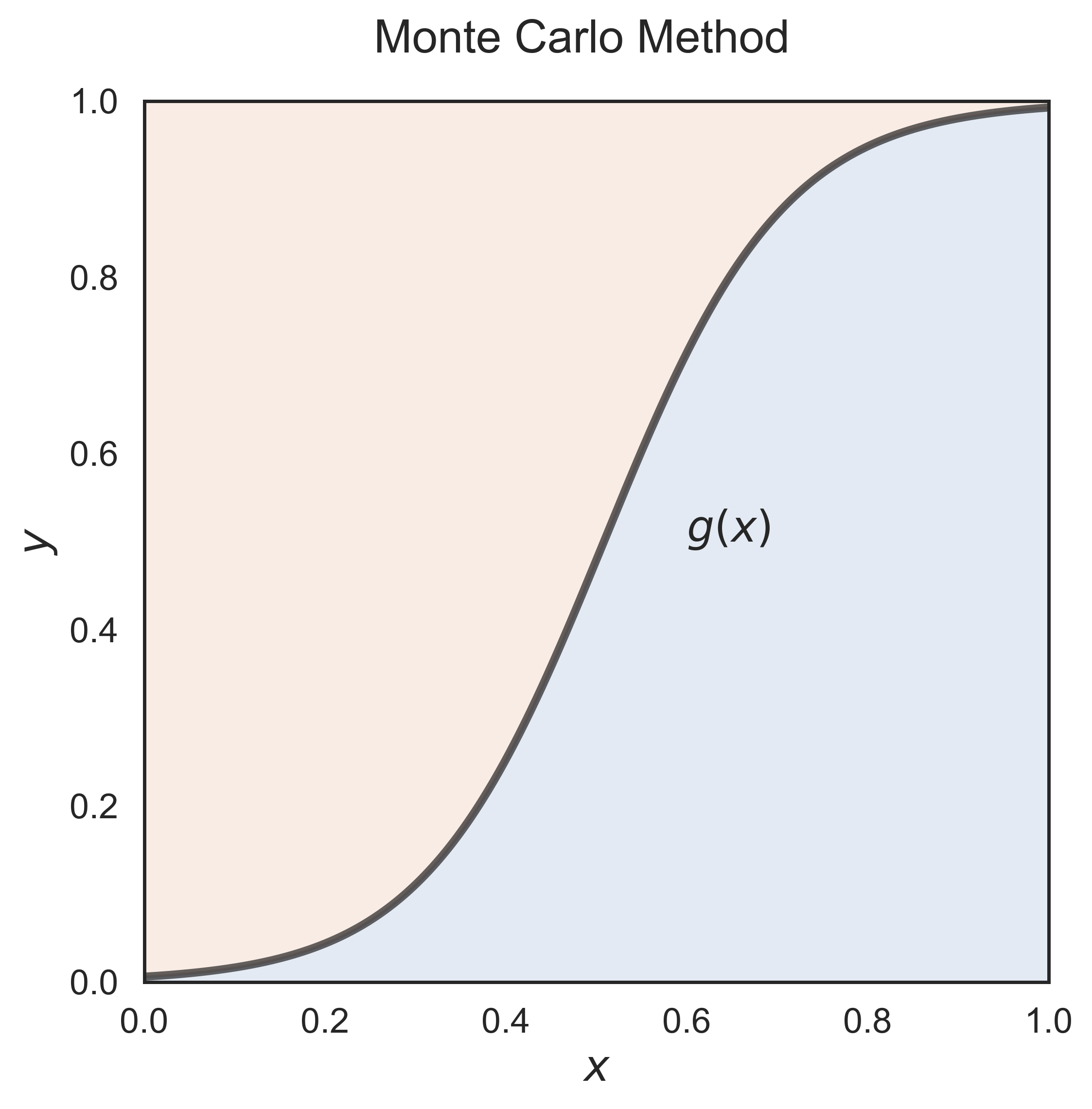
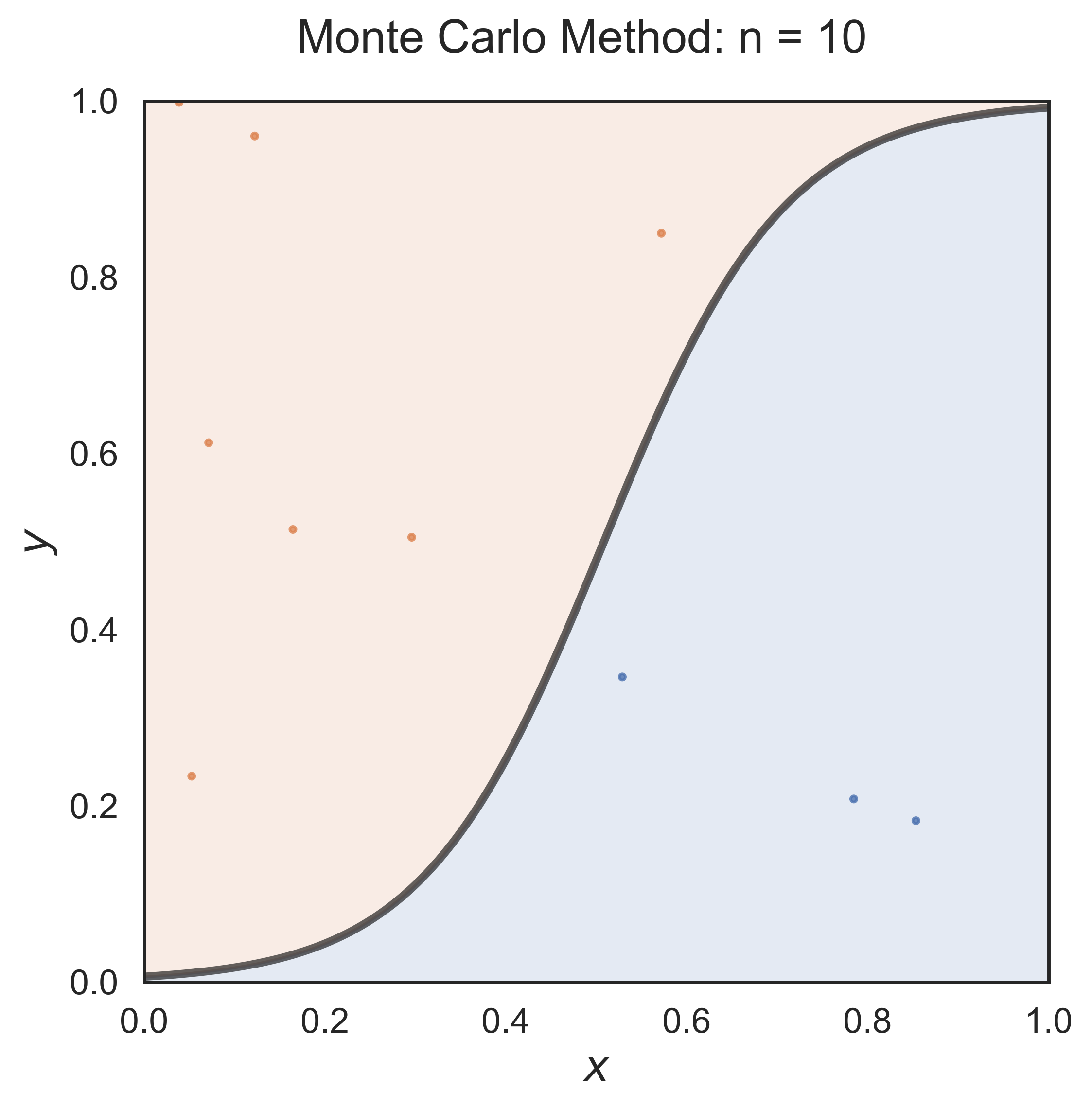
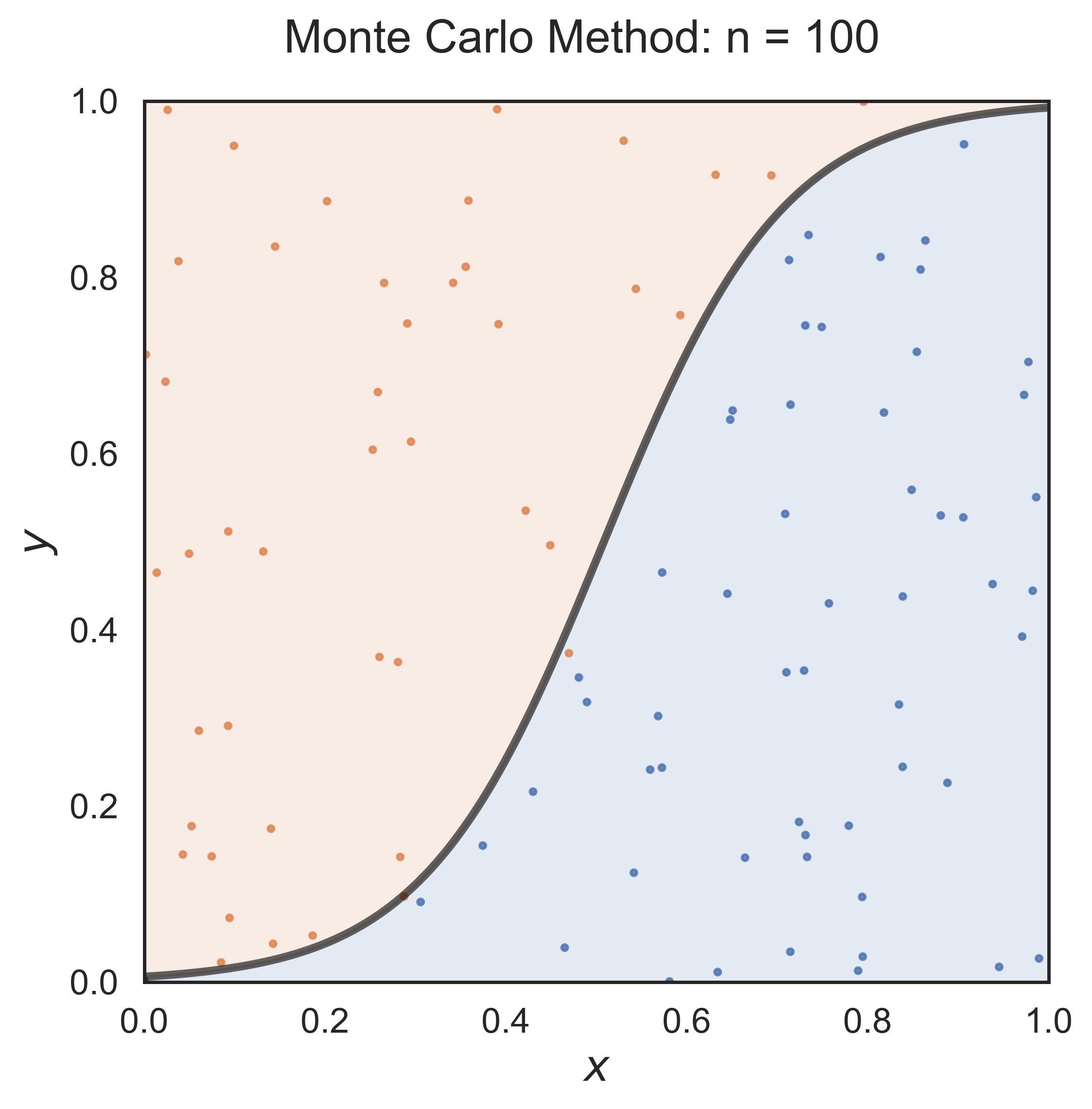
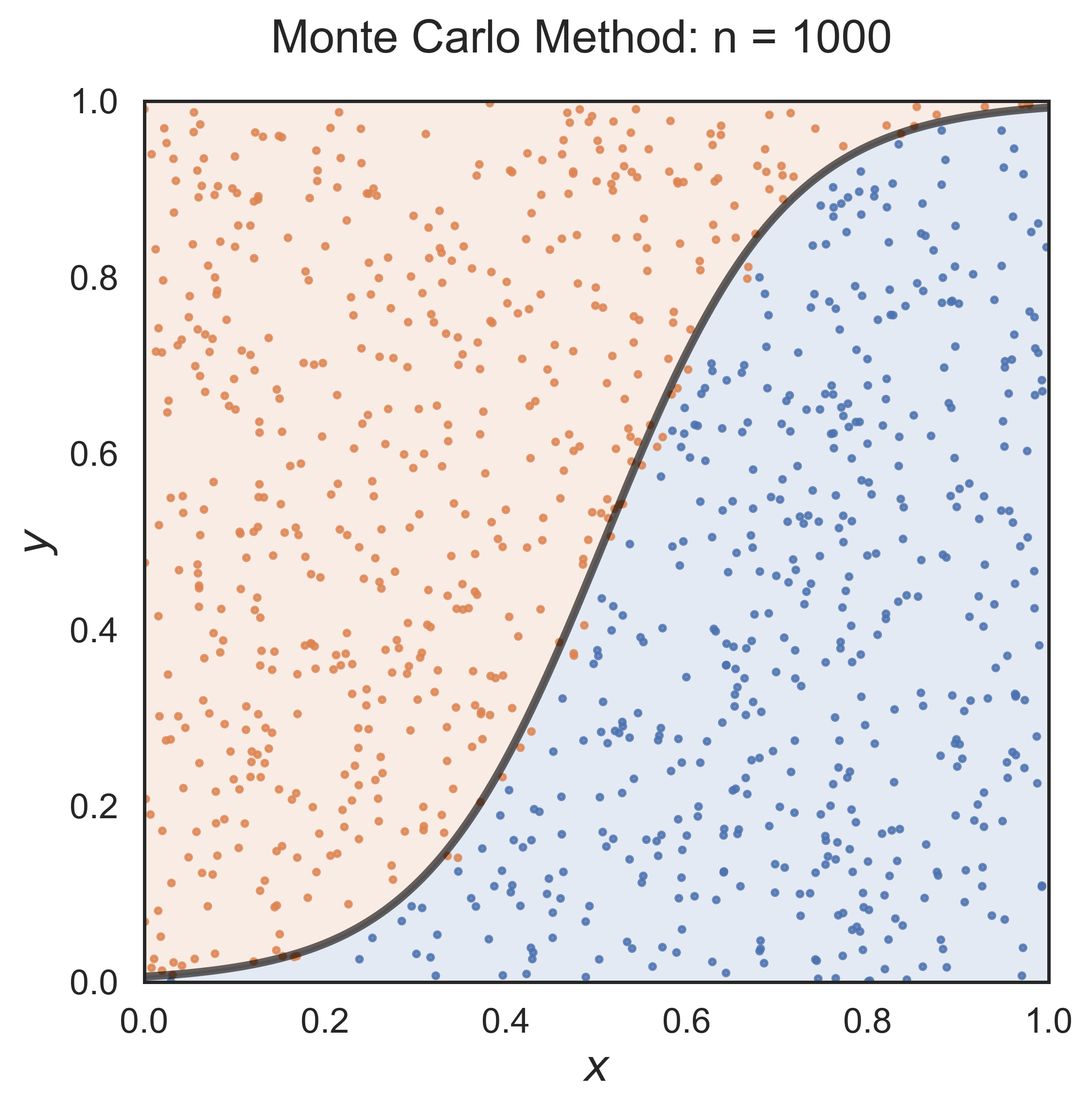
Monte Carlo Method
monte_carlo(n = 100, fsize = (6, 6), fs = 17)
Slides 0821
-
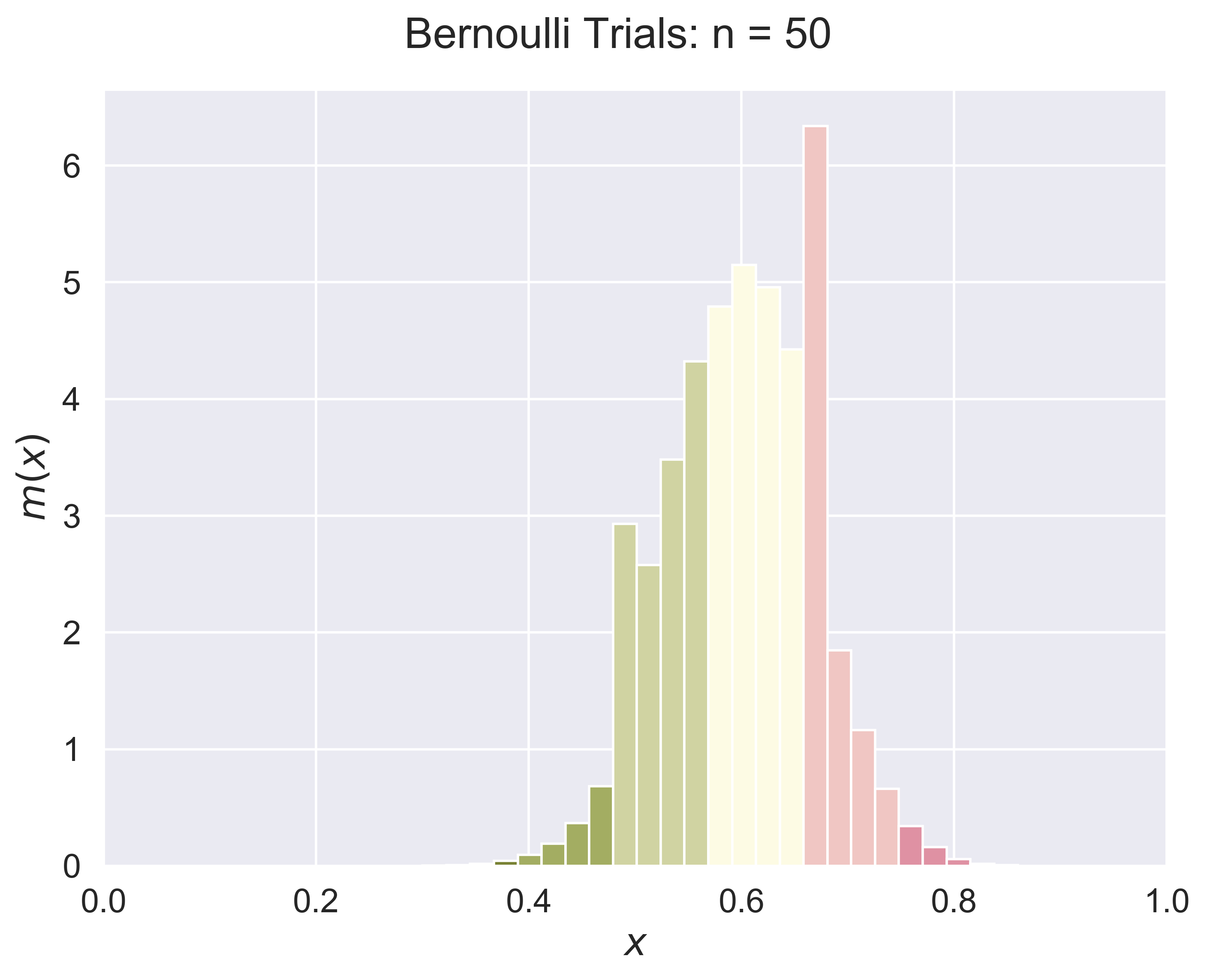
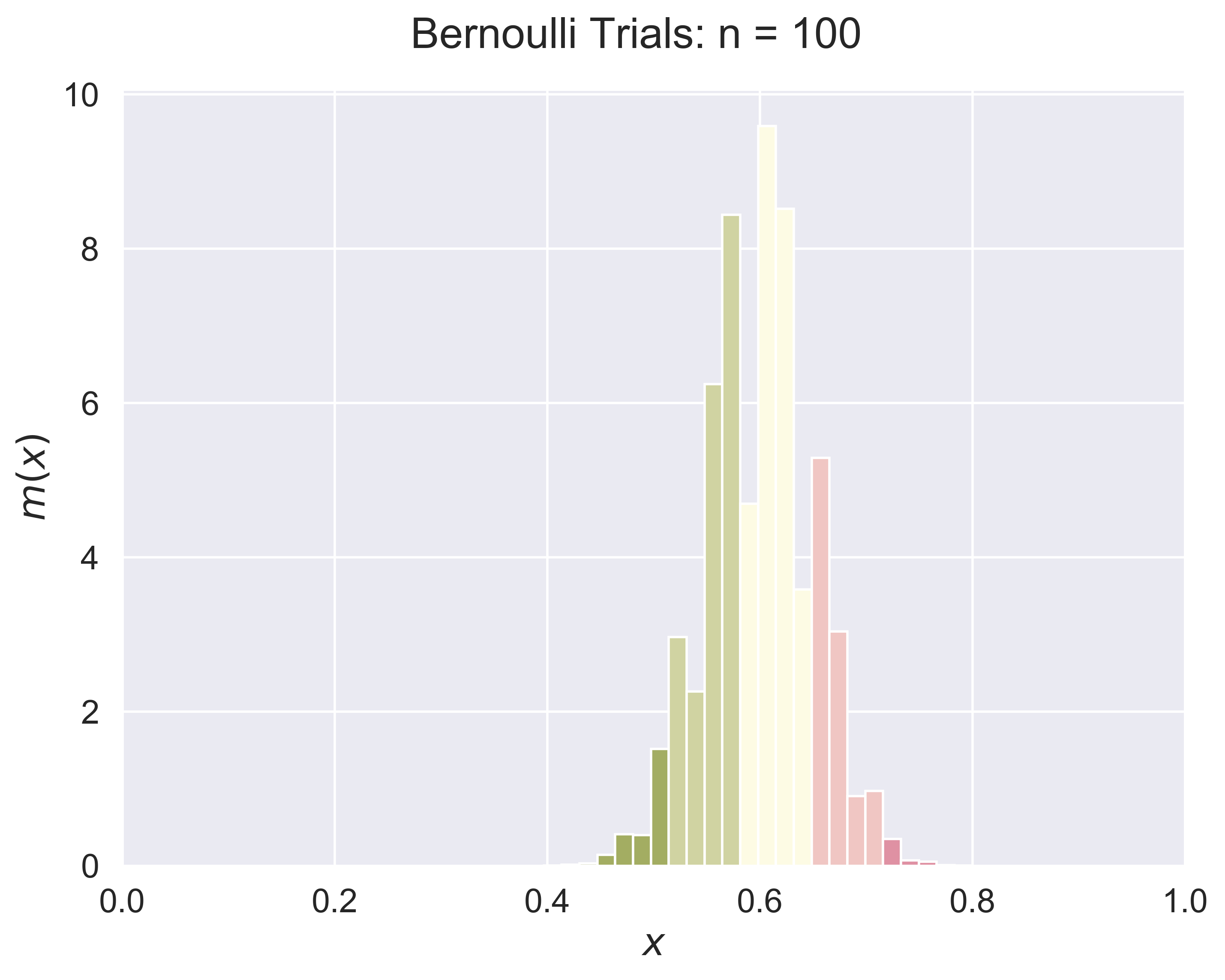
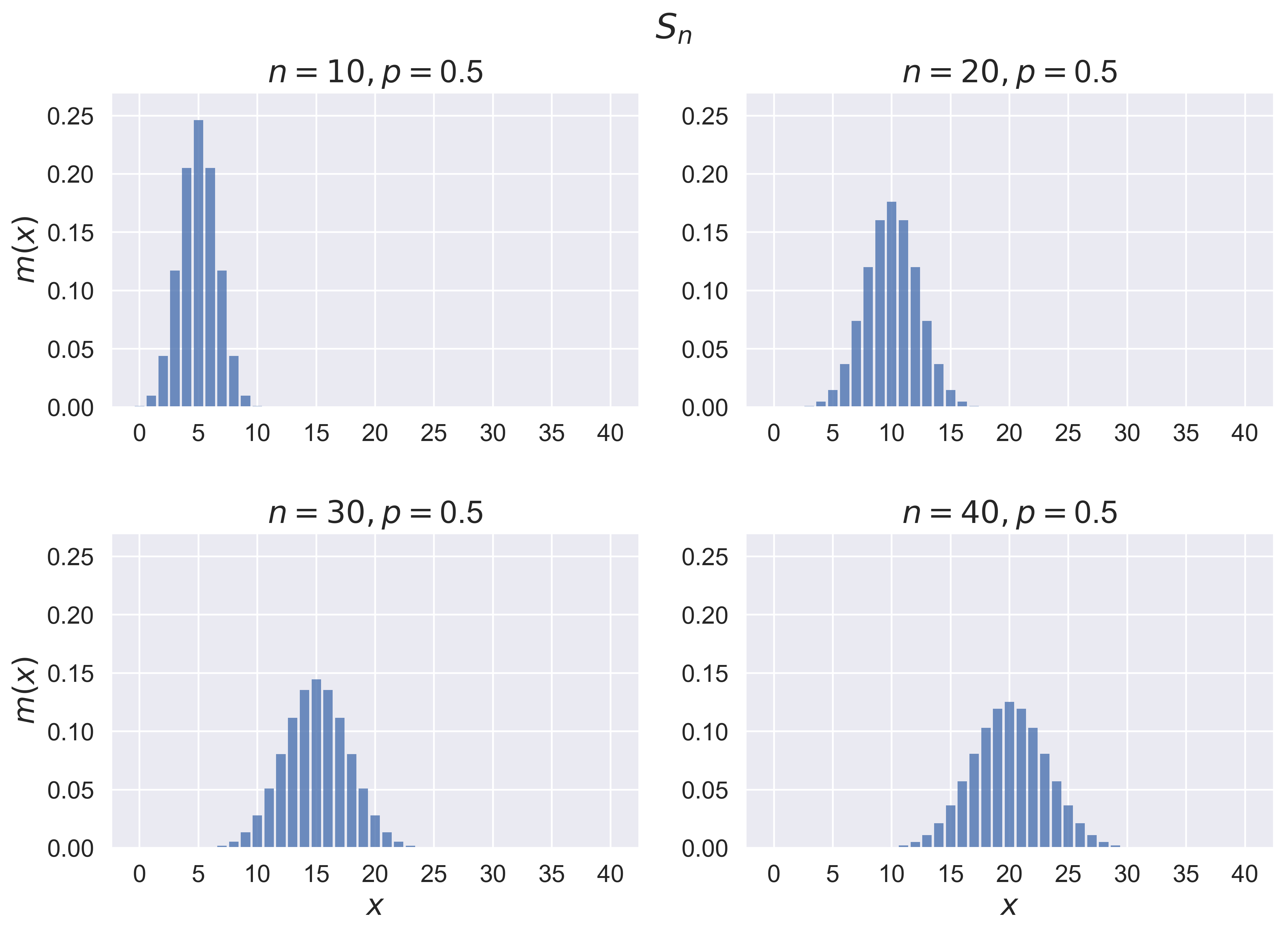
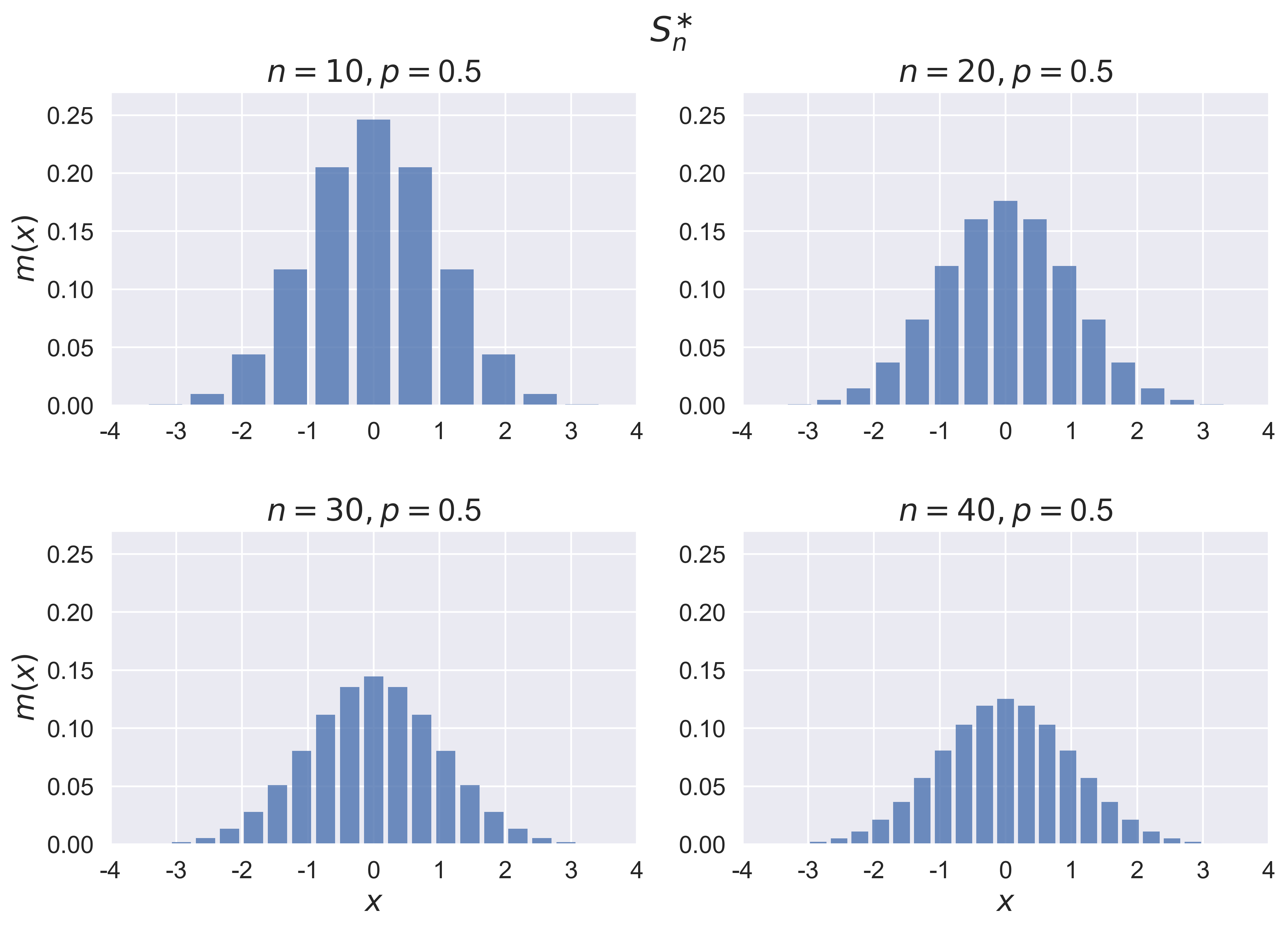
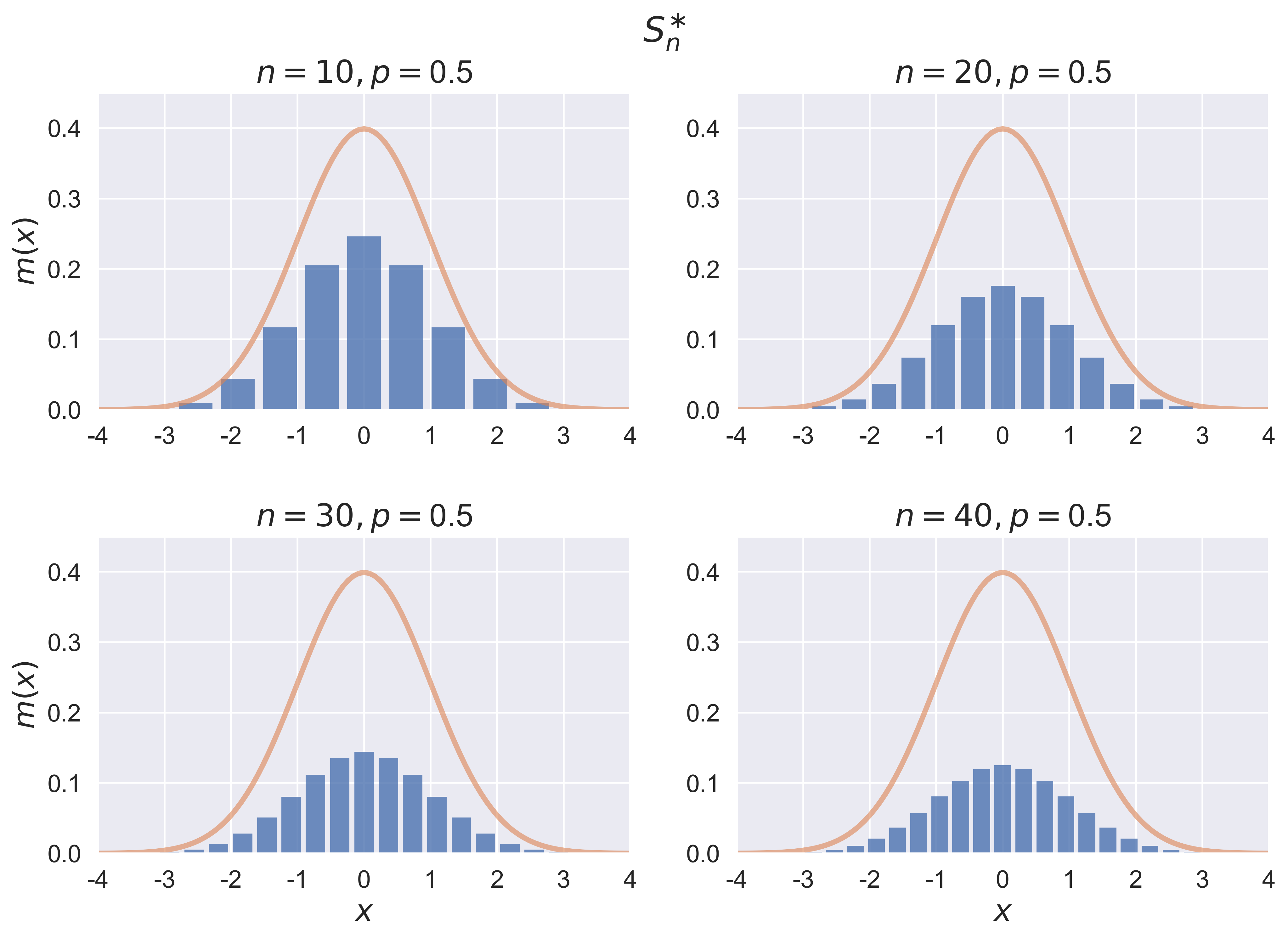
Central Limit Theorem for Bernoulli Trials
figure_bino_hist(job = 'original', p = 0.5, fsize = (12, 8), fs = 20)
figure_bino_hist(job = 'standardized', p = 0.5, fsize = (12, 8), fs = 20)
figure_bino_hist(job = 'standardized_normal', p = 0.5, fsize = (12, 8), fs = 20)
-
$x$ and $\sqrt{npq}b(n, p, k)$
Progress
The dates are consistent with the class.